6. Численное интегрирование

Необходимость вычисления значений определенных интегралов при моделировании возникает достаточно часто.

Формула Ньютона-Лейбница 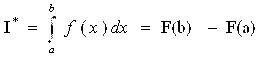(6.1)

Имеет ограниченное применение:

· во-первых, не позволяет вычислить интегралы от таблично заданной подынтегральной функции f(x);

· во-вторых, не всякая подынтегральная функция имеет первообразную F(x).

Численные методы интегрирования универсальны: позволяют вычислить значение определенного интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа ее задания или вида аналитического выражения.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b (Рис.6.1.).

Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются Квадратурными (формулами вычисления площади).

Рассмотрим получение и применение простейших формул.

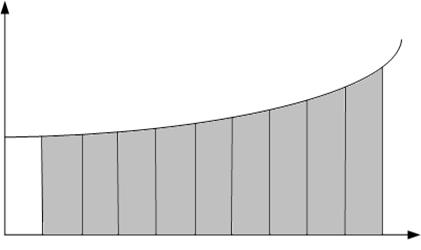
Рис. 6.1. Геометрический смысл определённого интеграла

Отрезок [a, b] делят на n необязательно равных частей – Элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x0, x1,…, xn – узлами сетки.

Если сетка равномерная, то – шаг сетки, при интегрировании – шаг интегрирования, а координата i-го узла вычисляется по формуле:

, (6.2)

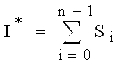
Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

(6.3)

Квадратурные формулы отличаются друг от друга способом оценки значения SI – площади элементарной криволинейной трапеции.

Рассмотрим получение простейших формул для часто используемой равномерной сетки.

< Предыдущая		Следующая >