5. Решение систем нелинейных уравнений (СНУ)
При моделировании задача нахождения решения системы алгебраических или трансцендентных уравнений является распространенной вычислительной задачей. Например, к решению таких систем сводятся расчеты фазового и химического равновесия многокомпонентных смесей, расчеты статических режимов многих технологических процессов и др.
Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:
![]() f1(x1, x2, …, xn) = 0
f1(x1, x2, …, xn) = 0
f2(x1, x2, …, xn) = 0 (5.1)
…
fn(x1, x2, …, xn) = 0
Эту систему можно записать в компактной, операторной форме:
F(X) = 0 (5.2)
Где
|
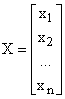
|
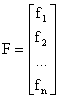
Решением системы называется набор значений ![]() ,
, ![]() (вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
(вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:
1 этап – отделение решений.
2 этап – уточнение всех или только нужных решений.
| < Предыдущая | Следующая > |
|---|