1. Введение
В настоящее время в науке и инженерной практике широко используется метод математического моделирования.
Математическим моделированием[1] Называется изучение реального объекта на ЭВМ с помощью математической модели этого объекта.
Например:
1. Совершенствование ядерного оружия путем расчетов на супер-ЭВМ. Удалось отказаться от испытаний ядерного вооружения.
2. Компьютерные тренажеры (симуляторы), созданные на основе математических моделей, появились сначала у военных, сейчас они широко применяются в производственном и учебном процессе.
Математическая модель – это приближенное математическое описание объекта (технологического процесса, реакции, явления и т. д.).
Примеры простейших моделей:
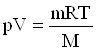 уравнение состояния идеального газа (1.1)
уравнение состояния идеального газа (1.1)
F =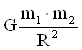 закон всемирного тяготения (1.2)
закон всемирного тяготения (1.2)
 закон сохранения энергии (1.3)
закон сохранения энергии (1.3)
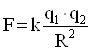 закон Кулона (1.4)
закон Кулона (1.4)
![]() закон сохранения энергии для фотона, (1.5)
закон сохранения энергии для фотона, (1.5)
где V – Частота излучения.
Сложные модели описывают объект точнее (Адекватнее[2]).
Математическое моделирование позволило исследовать на ЭВМ очень сложные процессы, такие, например, как глобальные климатические изменения в результате применения ядерного оружия (натурный эксперимент имеет катастрофические последствия).
В литературе математическое моделирование часто принято называть Вычислительным экспериментом.
Основные этапы математического моделирования:
1. Разработка модели – Формализация. Изучается в прикладных и фундаментальных науках.
2. Разработка метода (алгоритма) решения уравнения модели – Алгоритмизация. Изучается в вычислительной математике.
3. Создание программы – Программирование. Изучается в информатике.
4. Расчеты, анализ результатов – Практическое использование.
|

![]() Результат
Результат
|
![]() Программа
Программа
 |
 |
|
 | |
| |
|
 |
 |
|
Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом математического моделирования.
Например, пусть нужно найти R из уравнения (1.2) или (1.4), ![]() из уравнения (1.3) или c из уравнения (1.5). Что общего в этих задачах? То, что нужно решить уравнение вида:
из уравнения (1.3) или c из уравнения (1.5). Что общего в этих задачах? То, что нужно решить уравнение вида:
X 2 = a (1.6)
Вычислительная математика не рассматривает решения конкретных задач (1.2÷1.5), а изучает их решение в общем, абстрактном виде (1.6).
С точки зрения обычной математики точное решение уравнения (1.6) имеет вид:
![]() =
= ![]() ,
,
Причем если a > 0 , то два вещественных решения;
Если а = 0 , то тривиальное решение ![]() ;
;
Если а < 0, то вещественных решений нет.
Но знак ![]() не решает задачу, так как Не дает практического способа (алгоритма) вычисления значения Х для конкретного значения а.
не решает задачу, так как Не дает практического способа (алгоритма) вычисления значения Х для конкретного значения а.
Вычислительная математика предлагает следующий алгоритм вычисления X*:
1. Выбрать начальное значение Х, например ![]() =а. Это начальное приближение решения.
=а. Это начальное приближение решения.
2. Вычислять новые приближения решения Xi По формуле:
Xi = 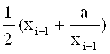 (1.7)
(1.7)
До достижения условия:
![]() e (1.8)
e (1.8)
Здесь i = 1,2,.. – номер вычисления - Итерации.
E – требуемая точность.
Пример. Нужно решить уравнение ![]() с точностью e=0,001.
с точностью e=0,001.
Зададимся ![]() ,
,
Вычислим первое приближение:  ,
,
Оценим точность | x1 – x0 | = ![]() .Требуемая точность не достигнута, нужно продолжить расчет.
.Требуемая точность не достигнута, нужно продолжить расчет.
Вычислим второе приближение: ![]() ,
,
Оценим точность ![]() .
.
Вычислим третье приближение: 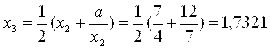 ,
,
Оценим точность ![]() .
.
Вычислим четвертое приближение: ![]() ,
,
Оценим точность ![]() − точность достигнута.
− точность достигнута.
Ответ: ![]() .
.
Точное значение (до 8 значащих цифр): ![]()
Рассмотренный пример демонстрирует Принципы, общие Для итерационных методов решения задач вычислительной математики:
1. Исходная задача (1.6) заменяется другой задачей – вычислительным алгоритмом по формулам (1.7), (1.8), где используются только арифметические операции +![]() . Принято называть (1.7) Формулой итерационного процесса (Итерационным процессом), (1.8) - Условием завершения итерационного процесса.
. Принято называть (1.7) Формулой итерационного процесса (Итерационным процессом), (1.8) - Условием завершения итерационного процесса.
2. Задача (1.7) содержит новый параметр i – Номер итерации. Очевидно, что Число итераций влияет на точность решения.
Если ![]() , то итерационный процесс является Сходящимся – позволяет получить решение исходной задачи (1.6).
, то итерационный процесс является Сходящимся – позволяет получить решение исходной задачи (1.6).
3. Решение, полученное итерационным методом, всегда является Приближенным, Так как точное решение получить невозможно – нужны бесконечные вычисления.
Важно подчеркнуть, что формула (1.7) получена из (1.6) путём Тождественных преобразований:
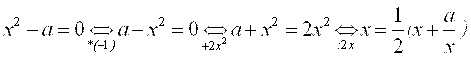
Но Не всякое тождественное преобразование позволяет получить сходящийся итерационный процесс.
Например:
A) 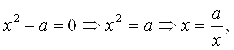
Выполним расчет при а=3:
![]() ;
; 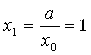 ;
;  ;
; ![]()
Итерационный процесс Не сходится; значения приближений Колеблются.
Б) ![]()
![]() ;
; ![]()
![]() …
…
Итерационный процесс Расходится.
Рассмотренный пример иллюстрирует один из видов численных методов – Итерационный.
Виды численных методов:
1. Прямые – решение получают за конечное число арифметических действий.
2. Итерационные – точное решение может быть получено Теоретически в виде предела Бесконечной сходящейся последовательности вычислений.
3. Вероятностные – методы случайного поиска решения (Угадывания).
Все виды численных методов позволяют получить только Приближенное решение задачи, то есть численное решение всегда содержит погрешность.
| Следующая > |
|---|