1.2.2. Условия сходимости и элементарные преобразования матрицы
Теорема. Если для приведенной системы (3) выполнено, по меньшей мере, одно из условий:
![]() или
или 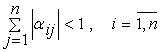 ,
,
То процесс итерации сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие. Для системы
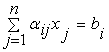 , (i = 1, 2, ..., n),
, (i = 1, 2, ..., n),
Метод итерации сходится, если выполнены неравенства:
![]() , (i = 1, 2, ..., n),
, (i = 1, 2, ..., n),
Т. е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Элементарными преобразованиями матрицы называются следующие ее преобразования:
– транспонирование, т. е. замена каждой строки столбцом с тем же номером;
– перестановка двух строк или двух столбцов;
– умножение всех элементов строки или столбца на любое число c, отличное от нуля;
–прибавление ко всем элементам строки или столбца соответствующих элементов параллельного ряда, умноженных на одно и то же число.
| < Предыдущая | Следующая > |
|---|