1.2.1. Метод простой итерации (метод Якоби)

Метод простой итерации [2], [5] рассмотрим на примере системы трех линейных алгебраических уравнений:

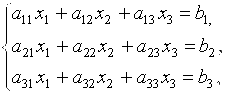(2)

Которую коротко можно записать в виде матричного уравнения:

Ах=b.

В исходной системе выделим диагональные коэффициенты аii ¹0 (где i =1, 2, 3).Предположим, что диагональные коэффициенты удовлетворяют условиям:

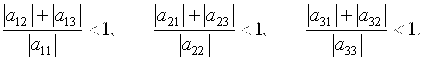
Если хотя бы одно из этих условий не выполняется, то следует провести элементарные преобразования матрицы (см. п.4).

Разрешим первое уравнение системы (2) относительно х1, второе –относительно х2, третье – относительно х3.

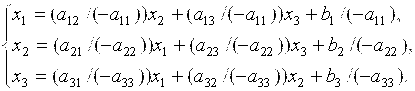
В результате получим эквивалентную систему:

(3)

Где при i¹j (i, j=1,2,…,n).

Систему (3) можем записать в матричной форме:.

Систему (3) будем решать методом простой итерации. В качестве нулевого приближения x(0) примем элементы столбца свободных членов:

X(0)=b, т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3.

Далее, находим первое приближение х(1), подставляя найденные значения нулевого приближения в систему (3):

Подставляя значения приближения х(1) в правую часть системы (3), получим:

– второе приближение.

Продолжая этот процесс далее, получим последовательность х(0), x(1), x(2),…, x(k),... приближений, вычисляемых по рабочим формулам:

В общем виде рабочие формулы для системы n-уравнений:

(4)

Если последовательность приближений имеет предел:

То этот предел является решением системы. Таким образом, с увеличением числа итераций растет точность получаемых корней. Однако можно не производить огромное количество итераций, а задать определенную точность e решения, при достижении которой итерационный процесс завершается. Условие окончания итерационного процесса можно записать в виде:

где i= 1,2,3,…, n.

Пример № 1. Методом простой итерации решить систему с точностью e= =10-3.

Решение.

1. Приведем систему к виду (3) . Для этого необходимо все диагональные элементы системы оставить в левой части уравнения, а остальные элементы перенести с противоположным знаком в правую часть. Разделим каждое из уравнений системы на соответствующий коэффициент, стоящий в левой части уравнения:

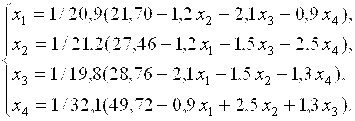
2. В качестве начального вектора x(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:

3. Вычисления будем вести до тех пор, пока не будет выполнено условие

где e = 10-3, i = 1,2,3,4.

Последовательно вычисляем: при k = 1:

Сравнивая полученные xi(1) с xi(0) , видим, что условия сходимости не выполняются. При k = 2:

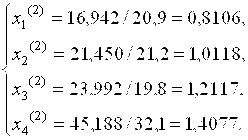
Сравнивая полученные xi(2) с xi(1), видим, что условия сходимости не выполняются. При k = 3

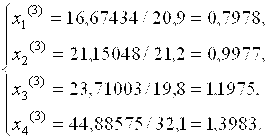
Сравнивая полученные xi(3) с xi(2) видим, что условия сходимости не выполняются. При k = 4:

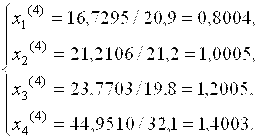
Для сравнения xi(4) с xi(3), найдем модули разностей значений

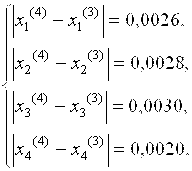
Так как все найденные значения модулей больше заданного числа

e = 10-3, продолжаем итерации. Получаем при k = 5:

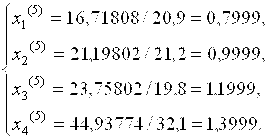
Находим модули разностей значений

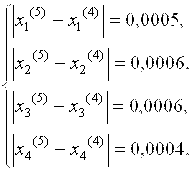
Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,7999, x2 = 0,9999, x3 = 1,1999, x4 = 1,3999.

< Предыдущая		Следующая >