56. Алгоритм ранжирования вершин графа, входящих в его контур
Вернемся к примеру с участниками шахматного турнира (табл. 5.1). В результате выделения из графа "доминирования – безразличия" для участников турнира контуров получен граф с двумя вершинами, соответствующими двум классам эквивалентности, первый из которых содержит пять сильнейших участников турнира A1, A2, ¼, A5. Для выделения лучшего участника турнира необходимо провести более детальный анализ элементов первого класса эквивалентности. При выполнении этого анализа будем использовать понятие силы M-го порядка (M = 1, 2, ¼).
Силой 1-го порядка участника турнира Aj (![]() ) называется сумма набранных им очков
) называется сумма набранных им очков
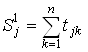 , (5.2)
, (5.2)
Где Tjk – результаты (0, 1/2, 1) партий J-го участника против остальных участников турнира (см. табл. 5.1) или элементы матрицы турнира T при нулевых элементах по главной диагонали:
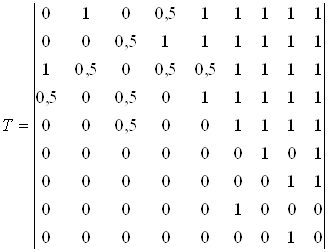 .
.
Силой 2-го порядка участника турнира Aj (![]() ) называется сумма очков, набранная с помощью промежуточных участников. Например, если Aj победил AL, а AL, в свою очередь, победил Ak (или сделал с ним ничью), то можно говорить о победе 2-го порядка игрока Aj над игроком Ak. Поскольку игроки Aj и Ak играют с каждым из (N – 2) оставшихся участников турнира, то число побед 2-го порядка над участником Ak может достигать (N – 2). Подсчитаем число побед 2-го порядка участника A3 над участником A5. Участник A3 выиграл у участника A1, который, в свою очередь, выиграл у A5. С участниками A2 и A4 партии A3 сыграны вничью, но и A2, и A4 выиграли у A5. Очевидно, что победа 2‑го порядка через участника A1 (выигрыш – выигрыш) более ценна, чем победы через участников A2 и A4 (ничья – выигрыш), поэтому последние победы желательно (или необходимо) учитывать с меньшим весом. Победы A3 над участниками A6 – A9 не идут в зачет его побед 2-го порядка, поскольку эти участники проиграли и участнику A5. Таким образом, в рассматриваемом примере при подсчете побед 2-го порядка участника A3 над A5 фигурирует третья строка и пятый столбец исходной матрицы турнира (табл. 5.1).
) называется сумма очков, набранная с помощью промежуточных участников. Например, если Aj победил AL, а AL, в свою очередь, победил Ak (или сделал с ним ничью), то можно говорить о победе 2-го порядка игрока Aj над игроком Ak. Поскольку игроки Aj и Ak играют с каждым из (N – 2) оставшихся участников турнира, то число побед 2-го порядка над участником Ak может достигать (N – 2). Подсчитаем число побед 2-го порядка участника A3 над участником A5. Участник A3 выиграл у участника A1, который, в свою очередь, выиграл у A5. С участниками A2 и A4 партии A3 сыграны вничью, но и A2, и A4 выиграли у A5. Очевидно, что победа 2‑го порядка через участника A1 (выигрыш – выигрыш) более ценна, чем победы через участников A2 и A4 (ничья – выигрыш), поэтому последние победы желательно (или необходимо) учитывать с меньшим весом. Победы A3 над участниками A6 – A9 не идут в зачет его побед 2-го порядка, поскольку эти участники проиграли и участнику A5. Таким образом, в рассматриваемом примере при подсчете побед 2-го порядка участника A3 над A5 фигурирует третья строка и пятый столбец исходной матрицы турнира (табл. 5.1).
Для подсчета числа очков, отражающих победу 2-го порядка игрока A3 над участником A5 можно рассмотреть произведение 3-й строки матрицы турнира T на 5-й столбец при условии, что по главной диагонали матрицы записаны нули:
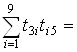 1 × 1 + 0,5 × 1 + 0 × 0,5 + 0,5 × 1 + 0,5 × 0 + 1 × 0 + 1 × 0 +1 × 0 +1 × 0 = 2.
1 × 1 + 0,5 × 1 + 0 × 0,5 + 0,5 × 1 + 0,5 × 0 + 1 × 0 + 1 × 0 +1 × 0 +1 × 0 = 2.
Анализ результатов расчета показывает, что произведение J-й строки на K‑й столбец достаточно удачно характеризует преимущество 2-го порядка J-го участника над K-м. При этом результаты "выигрыш – выигрыш", "выигрыш – ничья" (или "ничья – выигрыш") и "ничья – ничья" приносят победителю 2-го порядка соответственно очки: 1, 0,5 и 0,25. Если согласиться с такой численной оценкой указанных результатов, тогда получаем удобное обобщенное выражение для подсчета побед 2-го порядка J-го участника турнира над K-м
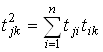 ,
, ![]() ,
, ![]() ,
,
Которое является произведением J-й строки и K-го столбца матрицы турнира T. Следовательно, число побед 2-го порядка любого участника турнира над любым другим участником этого турнира может быть определено с помощью матрицы T 2. В этом случае сила 2-го порядка J-го участника определяется как сумма элементов J-й строки матрицы T 2. Аналогично с помощью матрицы T M определяется сила M-го порядка для любого из участников турнира:
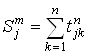 ,
,
Где ![]() – сила M-порядка J-го
– сила M-порядка J-го ![]() участника турнира;
участника турнира; ![]() (
(![]() ) – численный результат победы M-порядка J-го участника турнира над K-м (элемент J-й строки и K-го столбца матрицы T M); N – число участников турнира (число строк и столбцов матриц T, T 2, ¼, T M).
) – численный результат победы M-порядка J-го участника турнира над K-м (элемент J-й строки и K-го столбца матрицы T M); N – число участников турнира (число строк и столбцов матриц T, T 2, ¼, T M).
При ранжировании участников турнира удобно использовать не силу, а относительную силу M-го порядка ![]() каждого участника турнира
каждого участника турнира
 . (5.3)
. (5.3)
При неограниченном возрастании M относительные силы участников турнира стремятся к определенным пределам, которые обозначим как ![]() ,
, ![]() , и называют относительными силами участников турнира. Если
, и называют относительными силами участников турнира. Если ![]() >
> ![]() , то участник J доминирует или превосходит участника K.
, то участник J доминирует или превосходит участника K.
Используя введенные понятия, ранжируем участников турнира A1, A2, A3, A4, A5, попавших в первый класс эквивалентности. Результаты турнирной борьбы между этими участниками приведены в табл. 5.2, по распределению мест они полностью совпадают с табл. 5.1.
Таблица 5.2
|
A1 |
A2 |
A3 |
A4 |
A5 |
Очки |
Место | |
|
A1 |
1 |
0 |
0,5 |
1 |
2,5 |
1 – 3 | |
|
A2 |
0 |
0,5 |
1 |
1 |
2,5 |
1 – 3 | |
|
A3 |
1 |
0,5 |
0,5 |
0,5 |
2,5 |
1 – 3 | |
|
A4 |
0,5 |
0 |
0,5 |
1 |
2 |
4 | |
|
A5 |
0 |
0 |
0,5 |
0 |
0,5 |
5 |
Матрица T для рассматриваемого случая имеет вид:
 .
.
Сила первого порядка для участников A1, ¼, A5 в соответствии с выражением (5.2) задается вектором (2,5; 2,5; 2,5; 2; 0,5), а относительная сила – вектором (0,25; 0,25; 0,25; 0,20; 0,05). Таким образом, ранжирование по относительной силе первого порядка не отличается от ранжирования с помощью таблиц 5.1 и 5.2. Выполним ранжирование участников по относительной силе второго порядка. Имеем:

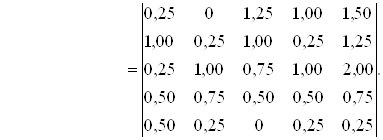
Из матрицы T 2 нетрудно получить вектор силы 2-го порядка S 2 = (4; 3,75; 5; 3; 1,25) и вектор относительной силы второго порядка ![]() = (0,235; 0,221; 0,294; 0,176; 0,074).
= (0,235; 0,221; 0,294; 0,176; 0,074).
Аналогично находим T 3, T 4, T 5 и векторы сил соответствующего порядка
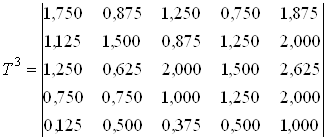 ;
;
S 3 = (6,500; 6,750; 8,000; 5,750; 2,500);
![]() = (0,2203; 0,2288; 0,2712; 0,1949; 0,0847);
= (0,2203; 0,2288; 0,2712; 0,1949; 0,0847);
 ;
;
S 4 = (12,1251; 12,250; 14,000; 9,750; 4,000);
![]() = (0,2326; 0,2350; 0,2686; 0,1871; 0,0767);
= (0,2326; 0,2350; 0,2686; 0,1871; 0,0767);
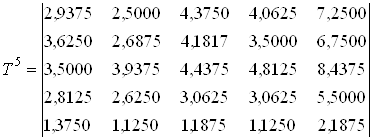 ;
;
S 5 = (21,1250; 20,7500; 25,1250; 17,0625; 7,0000);
![]() = (0,2320; 0,2279; 0,2759; 0,1874; 0,0769).
= (0,2320; 0,2279; 0,2759; 0,1874; 0,0769).
Анализ векторов относительной силы второго – пятого порядков показывает, что первое место занимает участник A3, четвертое и пятое – соответственно участники A4 и A5. Что касается второго и третьего мест, то здесь необходимы дополнительные расчеты.
Резюмируя итоги рассмотрения примера, приведем обобщенный алгоритм ранжирования вершин графа, входящих в его контур.
| < Предыдущая | Следующая > |
|---|