55. Алгоритмы поиска решений на графах отношений с трудновыделяемыми контурами

Для облегчения понимания материала вначале рассмотрим пример, а затем приведем общий алгоритм поиска решений в случаях, когда граф содержит трудновыделяемые контуры.

Пусть требуется ранжировать участников A1, A2, ¼, Aq некоторого шахматного турнира, результаты которого приведены в табл. 5.1, в которой хотя и приведено распределение мест среди участников, однако не определено, кто же из трех победителей турнира является сильнейшим.

Введем на множестве участников шахматного турнира отношение b "доминирование – безразличие". При этом выигрыш участника Ai у участника Aj будем рассматривать как доминирование участника Ai Над участником Aj: Ai B AJ, доминирование участника AI над участником Aj показана направленным ребром из вершины AI в вершину Aj, ничья или безразличие указано двунаправленной стрелкой. Петли на графе показывают, что отношение b рефлексивно, то есть каждый участник безразличен или равноценен самому себе. Из рисунка графа видно, что визуальное выделение контуров на графе – весьма сложная проблема. В таких случаях необходимо применение математических методов. Рассмотрим один из таких методов, основанный на том, что контуры графа, задающего бинарное отношение, порождают классы эквивалентности. Метод предусматривает задание отношения b с помощью булевой матрицы M [11], а затем получение N-й степени этой матрицы M N. Каждый класс эквивалентности отношения b состоит из элементов, которым в матрице M N бинарного отношения bN соответствуют одинаковые строки, и все вершины графа, соответствующие этим элементам, принадлежат одному контуру.

Таблица 5.1

	A1	A2	A3	A4	A5	A6	A7	A8	A9	Очки	Место
A1		1	0	0,5	1	1	1	1	1	6,5	1 – 3
A2	0		0,5	1	1	1	1	1	1	6,5	1 – 3
A3	1	0,5		0,5	0,5	1	1	1	1	6,5	1 – 3
A4	0,5	0	0,5		1	1	1	1	1	6	4
A5	0	0	0,5	0		1	1	1	1	4,5	5
A6	0	0	0	0	0		1	0	1	2	6 – 7
A7	0	0	0	0	0	0		1	1	2	6 – 7
A8	0	0	0	0	0	1	0		0	1	8 – 9
A9	0	0	0	0	0	0	0	1		1	8 – 9

Построим булеву матрицу бинарного отношения b, заданного графом на рис. 5.9. В этой матрице каждой стрелке графа из вершины Ai () (или каждой победе и ничьей в табл. 5.1) должна соответствовать единица. Единицы должны находиться и по главной диагонали матрицы, поскольку каждый участник безразличен (или равноценен) самому себе.

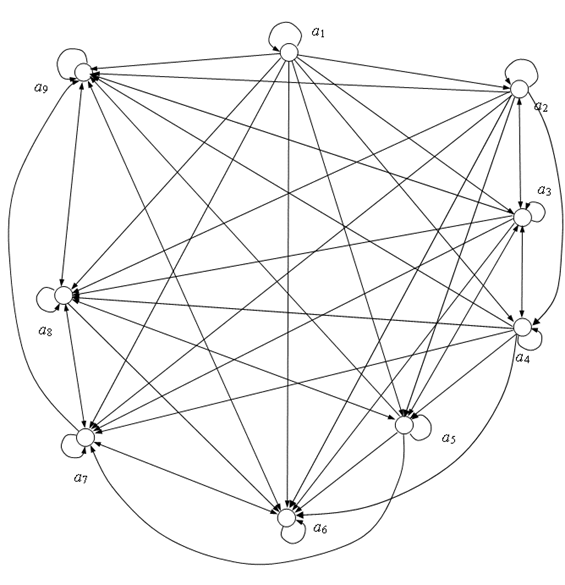
Рис. 5.9. Граф отношения "доминирование – безразличие" для участников турнира

Булева матрица бинарного отношения b, заданного графом на рис. 5.9, имеет вид:

.

Найдем последовательность матриц M 2, M 3, ¼, M 9, соответствующих степеням бинарного отношения b2, b3, ¼, b9. При умножении двух матриц N и M, соответствующих бинарным отношениям r и b и имеющих размеры N × N, элемент  Vkl матрицы V = N × M вычисляется по формуле

, , (5.1)

Где , , (, ) – соответственно элементы матриц V, N, M, при этом в выражении (5.1) используется обычная операция булевого умножения и операция дизъюнкции. Перемножая матрицы M × M, получим матрицу M2, задающую бинарное отношение b2,

Далее имеем:

.

.

Поскольку матрица бинарного отношения M 9 имеет две группы одинаковых строк, то граф, приведенный на рис. 5.9, имеет всего два контура. В первый контур входят вершины A1, A2, ¼, A5, а во второй – вершины A6, A7, A8, A9. Учитывая результаты турнира, приведенные в табл. 5.1, можно говорить о том, что получено два класса эквивалентности, первый из которых составляют более сильные шахматисты, а второй – неудачники турнира. Следовательно, в результате выделения контуров исходный граф с девятью вершинами может быть преобразован к графу с двумя вершинами, соответствующими двум классам эквивалентности.

Таким образом, из рассматриваемого примера и предыдущего материала подраздела следует, что алгоритм поиска решений в случаях, когда граф отношения содержит трудновыделяемые контуры, следующий:

1. По графу бинарного отношения b, содержащего N вершин, строят булеву матрицу M бинарного отношения.

2. Вычисляют степени матрицы M: M 2, M 3, ¼, M N, соответствующие бинарным отношениям b2, b3, ¼, bN.

3. В матрице M N определяют группы одинаковых строк. Число групп строк соответствует числу контуров в графе, а номера строк указывают вершины графа, которые входят в контур.

4. Вершины, принадлежащие одному контуру в графе бинарного отношения, относят к одному классу эквивалентности и заменяют одной вершиной.

5. Проверяют, удовлетворяет ли полученный граф одному из отношений порядка. Если удовлетворяет, то строят диаграмму отношения порядка и применяют алгоритмы поиска решений с использованием диаграмм, описанные в пункте 5.7.1. В противном случае переходят к п. 6 алгоритма.

6. Проверяют возможность внесением дополнительной информации достроить граф до графа одного из отношений порядка. Если такая возможность существует, то достраивают граф и переходят к п. 5. В противном случае переходят к следующему пункту алгоритма.

7. Из графа удаляют все вершины, которые соответствуют доминируемым объектам (элементам, альтернативам и т. д.).

8. Вносят в граф дополнительную информацию о доминировании и (или) безразличии оставшихся недоминируемых элементах множества, на котором задано бинарное отношение b.

9. Проверяют наличие в графе единственной недоминируемой вершины (или объекта, ей соответствующего), которая доминирует все остальные вершины. Если такая вершина существует, то лучший объект определен, в противном случае переходят к п. 7 алгоритма.

10. Конец.

В результате применения алгоритмов пунктов 5.8.1, 5.8.2 могут быть выделены в качестве лучших вершины графов, соответствующие классам эквивалентности или контурам графов. В этом случае возникает задача ранжирования элементов класса эквивалентности или вершин контура графа. Рассмотрим один из алгоритмов, позволяющих решить эту задачу.

< Предыдущая		Следующая >