37. Решение матричных игр методами линейного программирования
Математическое программирование – это раздел математики, предназначенный для решения задач, связанных с определением программ (планов, распределений, расписаний и т. д.), которые оптимальны с точки зрения некоторой целевой функции или критерия оптимальности. Обычно определение оптимальной или наилучшей программы состоит в выборе из множества допустимых программ той, которая минимизирует или максимизирует заданный критерий. Множество допустимых программ описывается с помощью ограничений, задаваемых в виде уравнений и неравенств. Если функция цели, или некоторые ограничения нелинейны, то рассматриваемая задача является задачей нелинейного программирования. Если функция цели и все ограничения линейны, то мы имеем дело с задачей линейного программирования.
Общая задача линейного программирования в математической форме описывается следующим образом.
Определение. Общей задачей линейного программирования называется задача максимизации (или минимизации) линейной формы
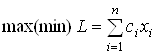(3.48)
При ограничениях
, 
;
, 
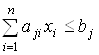; (3.49)
, 
,
Где 
– вектор неизвестных величин, изменяя который можно улучшать описываемую систему или объект; он имеет ряд названий: план задачи, вектор решения, вектор управления, стратегия, поведение и т. д.; (3.48) – целевая функция (показатель эффективности, критерий оптимальности, функционал задачи, функция цели и т. д.), она позволяет выбрать наилучший вариант, при котором выражение (3.48) достигает экстремального значения. Совокупность ограничений (3.49) определяет область допустимых решений для вектора X.
Словесно общую задачу линейного программирования можно сформулировать так: требуется найти максимум (или минимум) линейной формы от N переменных при M ограничениях в виде неравенств или равенств.
В приложениях часто используется симметричная форма задач линейного программирования:
Максимизировать линейную форму
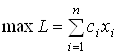(3.50)
При ограничениях
, 
; (3.51)
, . (3.52)
Или минимизировать линейную форму
(3.53)
При ограничениях
, 
; (3.54)
, 
. (3.55)
Рассмотрим приведение матричной игры к задаче линейного программирования.
Пусть задана матричная игра A порядка N ´ M
.
При этом полагаем, что чистая нижняя и верхняя цены игры положительны, т. е. a > 0 и b > 0, или отрицательны. Если a < 0, а b > 0, то не исключается возможность того, что цена игры V равна нулю, что недопустимо в последующих преобразованиях. В таком случае к каждому элементу матрицы необходимо добавить такую положительную константу K, чтобы a и b стали одного знака. При таком добавлении константы K компоненты смешанных стратегий обоих игроков не изменятся, а цена игры возрастет на K единиц.
Согласно теореме 3.3 оптимальные смешанные стратегии игроков X0, Y0 удовлетворяют соотношениям (3.15) – (3.18):
, 
;
|
;
, ;
.
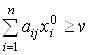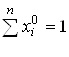Разделим обе части каждого из соотношений (3.56) на цену игры V и, введя обозначения 
, 
, 
, 
, получим:
, 
;
;
, ;
.
Первый игрок стремится в течение партии увеличить цену игры V или, что то же, минимизировать ее обратную величину 
. Это равносильно минимизации линейной формы
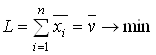
При ограничениях
, .
Такая формулировка действий первого игрока в математической форме совпадает с формой записи задачи линейного программирования при минимизации целевой функции.
Второй игрок с помощью своей смешанной стратегии 
или стратегии 
стремится уменьшить цену игры V или максимизировать ее обратную величину . Это равносильно максимизации линейной формы
При ограничениях
, .
Такое математическое описание действий второго игрока совпадает формально с формой записи задачи линейного программирования при максимизации целевой функции.
Итак, мы имеем две взаимосвязанных задачи линейного программирования, которые относятся к классу двойственных симметричных задач линейного программирования.
Определение. Две задачи линейного программирования называются двойственными симметричными задачами, если они могут быть сформулированы следующим образом
Задача 1 (прямая задача).
Найти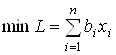 
при ограничениях
, 
;
, .
Задача 2 (двойственная задача).
Найти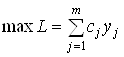 
при ограничениях
, 
,
, .
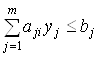Заметим, что в определение двойственных задач обе исходные задачи входят равноправно, т. е. любая из них может быть и прямой, и двойственной.
Сопоставляя математические формулировки прямой и двойственной задач линейного программирования, можно отметить следующие взаимосвязи:
– если прямая задача на минимум, то двойственная – на максимум, и наоборот;
– коэффициенты 
и 
целевых функций прямой и двойственной задач являются свободными членами ограничений соответственно двойственной и прямой задач;
– в прямой задаче число переменных N и число ограничений M равно соответственно числу ограничений N и числу переменных M двойственной задачи;
– если прямая задача на минимум, то ее ограничения описываются системой неравенств вида "≥"; в двойственной задаче на максимум ограничения описываются системой неравенств "£";
– в обеих задачах линейного программирования все переменные неотрицательны.
Двойственные симметричные задачи линейного программирования обладают важным свойством, которое доказано в теореме двойственности.
Теорема 3.6 (теорема двойственности) [6]. Если одна из двойственных задач имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем экстремальные значения целевых функций равны: 
. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений второй задачи противоречива.
Таким образом, любая матричная игра может быть сведена к одной из двух двойственных симметричных задач линейного программирования, а затем решена с помощью известных методов, в частности, с использованием пакетов, например, Matlab или Excel.
| < Предыдущая | Следующая > |
|---|
