16. Критерий Ходжа-Лемана

Критерий Байеса-Лапласа дает более оптимистичные прогнозы, чем максиминный критерий, однако он предполагает и более высокий уровень информированности, и многократные реализации.

Критерий Байеса-Лапласа надежен только тогда, когда точно известны вероятности появления состояний внешней среды, однако на практике точные числа, как правило, отсутствуют. Это ослабляет доверие к критерию и заставляет обращаться к более надежному максиминному критерию, который гарантирует определенный минимум. Этот гарантированный минимум можно попытаться увеличить за счет использования взвешенной линейной комбинации рассматриваемых критериев:

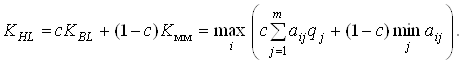(1.16)

С помощью параметра С , с одной стороны, выражается степень доверия к используемому распределению вероятностей, а с другой – степень нежелательности появления очень малых значений. Если степень доверия велика и число реализаций принятого решения значительно, то акцентируется критерий KBL, в противном случае предпочтение отдается максиминному критерию. Поскольку числовая оценка степени доверия к используемому распределению вероятностей и степени нежелательности появления малых значений обычно затруднена, то выбор параметра C, как правило, субъективен. Во многих случаях полагают, что C = 0,5. При C = 1 критерий KHL переходит в критерий Байеса-Лапласа, а при C = 0 превращается в максиминный критерий.

< Предыдущая		Следующая >