18. Умножения вероятностей

В задачах, использующих вероятностные количественные характеристики, приходится по вероятностям одних событий оценивать вероятности других событий. Для этого используются различные соотношения, в основе которых лежат теоремы сложения и умножения вероятностей.

Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет; в противном случае такие события называются зависимыми. Например, вероятность события того, что во второй раз из урны, содержащей белые и черные шары, будет вынут белый шар, не зависит от того, какой шар был вынут в первый раз, если он был возвращен обратно. Однако если первый шар не был возвращен обратно, то результат второго извлечения уже будет зависеть от первого, ибо состав шаров в урне уже изменится в зависимости от результата первого извлечения.

Вероятность произведения независимых событий A и B равна произведению вероятностей этих событий:

. (16.1)

Пример 16.1. Алмазы, возможно, вскоре станут использовать в качестве полупроводников в спутниках связи. Эксперты предсказывают, что алмазные микросхемы будут более быстродействующими, термо - и радиационностойкими, что особенно важно для приборов, работающих в космосе. По оценкам экспертов, вероятности этих трех событий равны 0,9; 0,9 и 0,95 соответственно. Предполагается, что обсуждением проекта по разработке алмазных микросхем стоит вести лишь в том случае, если имеется хотя бы 70% уверенности в том, что они будут обладать всеми тремя указанными свойствами. Должен ли обсуждаться проект?

Решение. Пусть A – событие, состоящее в том, что алмазные микросхемы будут более быстродействующими, B – событие, состоящее в том, что алмазные микросхемы будут более термостойкими, C – событие, состоящее в том, что алмазные микросхемы будут более радиационностойкими. Поскольку события A, B и С независимы, то, используя теорему умножения вероятностей (2.3), получим

.

Таким образом, поскольку 0,7695>0,7, то предложенный проект следует обсуждать.

Пример 16.2. Дана электрическая цепь:

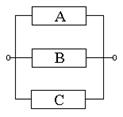
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдут из строя все элементы цепи, т. е. и элемент А, и элемент В, и элемент С. При помощи алгебры событий разрыв цепи можно описать следующим образом: . Поскольку эти события независимы, то

Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается или .

Вероятность произведения двух событий A и B равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже имело место:

. (16.2)

Пример 16.3. Одна из наиболее сложных проблем рыночных исследований – отказ потребителей отвечать на вопросы о потребительских предпочтениях, либо, если опрос проводится по месту жительства, – отсутствие их дома на момент опроса. Предположим, что исследователь рынка с вероятностью в 0,94 верит, респондент согласится отвечать на вопросы анкеты, если окажется дома. Он также полагает, что вероятность того, что этот человек будет дома, равна 0,65. Имея такие данные, оцените процент заполненных анкет.

Решение. Пусть A – событие того, что респондент окажется дома. Вероятность этого события . Пусть B – событие того, что респондент согласится отвечать на вопросы. По условию задачи задана условная вероятность , т. е. вероятность того, что он согласится отвечать на вопросы, если он будет дома. Тогда, согласно теореме умножения вероятностей зависимых событий (2.4), вероятность того, что человек будет дома и согласится отвечать на вопросы, будет равна

,

Т. е. процент заполненных анкет будет равен 61%.

Пример 16.4. Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,8. Какова вероятность поражения цели, если в 2% случаях бывают осечки, т. е. в 2% случаях выстрела не происходит?

Решение. Пусть событие В состоит в том, что выстрел произошел, тогда событие означает противоположное событие, т. е. что произошла осечка. По условию P()=0,02, отсюда получаем P(B)=1–P()=0,98. По условию задачи PB(A)=0,8. Поражение цели означает совмещение событий В и А, т. е. что выстрел произойдет и даст попадание. Поэтому

P(AB) = P(B)PB(A) = 0,98×0,8 = 0,784.

Пример 16.5. В коробке девять одинаковых радиоламп, три из которых были в употреблении. В течение рабочего дня мастеру для ремонта пришлось взять две радиолампы. Какова вероятность того, что обе радиолампы были в употреблении?

Решение. Вероятность того, что первая взятая радиолампа была в употреблении (событие А), равна P(A)=3/9. После того как событие А произошло в коробке осталось 8 радиолам, из которых две были в употреблении. Поэтому для события В, состоящего в том, что вторая радиолампа была в употреблении, условная вероятность PA(B)=2/8. Следовательно, вероятность появления двух ламп, бывших в употреблении, равна:

P(AB) = P(A)PA(B) = .

Заметим, что данную задачу можно решить и комбинаторным способом:

P(AB) = .

Понятие условной вероятности позволяет естественным образом определить независимость событий. Говорят, что событие А независимо от события В, если имеет место равенство

PB(A) = P(A),

Т. е. если наступление события В не влияет на вероятность наступления события А. Если событие А не зависит от В, то и событие В также не зависит от А. Таким образом, свойство независимости взаимно. Поэтому за определение независимости двух событий А и В можно принять условие (16.1).

Упражнения

16.1. Вероятность того, что завтра цены на потребительские товары вырастут, равна 0,3; вероятность того, что завтра поднимется цена на серебро, равна 0,2, а вероятность одновременного роста цен на потребительские товары и серебро составляет 0,06. Являются ли цены на потребительские товары и серебро независимыми друг от друга? Поясните ответ.

Ответ. Да, т. к. 0,3×0,2=0,23.

16.2. Иностранная фирма, производящая автомобили, интересуется российским рынком. Для изучения вкусов потенциальных покупателей проводится опрос, в котором выясняются наиболее желательные характеристики автомобиля. Предположим, что результаты опроса показали: 35% потенциальных покупателей в основном оценивают автомобиль по его техническим характеристикам, 50% – по его дизайну, 25% – считают важным и то, и другое. Основываясь на этой информации, ответьте, являются ли два вида предпочтений потенциальных покупателей независимыми друг от друга? Объясните почему?

Ответ. Нет, не являются, т. к. 0,35×0,5¹0,25.

16.3. Аудиторская фирма размещает рекламу в журнале "Коммерсант". По оценкам фирмы, 60% людей, читающих журнал, являются потенциальными клиентами фирмы. Выборочный опрос показал также, что 85% людей, которые читают журнал, помнят о рекламе фирмы, помещенной в конце журнала. Оцените, чему равен процент людей, которые являются потенциальными клиентами фирмы и могут вспомнить ее рекламу?

Ответ. 0,85×0,6=0,51, т. е. 51%.

16.4. Консультационная фирма получила приглашение для выполнения двух видов работ от двух международных корпораций. Руководство фирмы оценивает вероятность получения заказа от фирмы А (событие А) равной 0,45. Также, по мнению руководителей фирмы, в случае, если фирма заключит договор с компанией А, то с вероятностью в 90% компания В даст фирме консультационную работу. С какой вероятностью компания получит оба заказа?

Ответ. 0,45×0,9=0,405.

16.5. Вероятность наступления события А в каждом опыте одинакова и равна 0,4. Опыты производятся последовательно до наступления события А. Определить вероятность того, что понадобится ровно 3 опыта.

Ответ. 0,4×0,4×0,6=0,096.

< Предыдущая		Следующая >