8. Глоссарий

Биномиальное распределение с параметрами N И P – Вычисление вероятности того, что случайная величина принимает значения M=0, 1,…, N.

Вариационный ряд – Последовательность элементов выборки, расположенных в неубывающем порядке (одинаковые элементы записываются последовательно друг за другом).

Вероятность произведения двух независимых событий – Произведение вероятностей этих событий.

Вероятность события -- Отношение числа исходов M события А к общему числу элементарных событий N.

Возможные значения случайной величины – числа ¦(w).

Выборка – Последовательность значений из генеральной совокупности;

- объема K - часть, состоящая из K элементов генеральной совокупности;

- репрезентативная – позволяет адекватно описать случайную величину

- случайная объема N – Последовательность N Независимых случайных величин из генеральной совокупности.

Выборочная дисперсия – величина, равная сумме квадратов разностей между значением случайной величины и ее математическим ожиданием, деленная на объем выборки.

Выборочное Среднее – Число, равное сумме значений случайной величины, деленной на объем выборки.

Генеральная совокупность – Конечная или бесконечная совокупность наблюдений над случайной величиной.

Геометрическое определение вероятности – Отношение площади S(A), соответствующей событию A, к площади всей области W.

Гипергеометрическое распределение – Вычисление вероятности того, что случайная величина примет заданное значение через число сочетаний.

Гипотеза альтернативная – Гипотеза, конкурирующая с основной;

-основная – Гипотеза, которая проверяется;

-статистическая – Предположение относительно параметров или закона распределения случайной величины.

Гистограмма – Представление статистического ряда на плоскости.

Дискретная случайная величина - Множество возможных значений образует конечную или бесконечную последовательность чисел, т. е. конечно или счетно.

Дисперсия случайной величины X – момент второго порядка случайной величины (x - M(x)).

Доверительная вероятность – Вероятность, с которой производится оценка параметров.

Доверительный интервал – Область значений, при которых основная гипотеза принимается.

Дополнение Множества A – разность между всем множеством S и множеством А, которое является частью S.

Достоверное Событие W – всегда наступает в условиях данного эксперимента.

Закон трех сигм – значения случайной величины ξ, имеющей нормальное распределение с параметрами M и σ, содержатся в интервале

Кривая распределения – график плотности вероятности.

Критерий значимости – Вероятность ошибки 1-го рода.

Критерий

- согласия – Правило, в соответствии с которым принимается решение;

- Колмогорова – Проверка гипотезы о совпадении функций распределения.

Математическое ожидание дискретной случайной величины x – сумма ряда из произведений возможных значений Xi на их вероятности Pi.

Множество – некоторая совокупность объектов, называемых элементами множества.

Множество конечное – состоящие из конечного числа элементов, в противном случае – Бесконечное множество.

Момент второго порядка случайной величины x – математическое ожидание квадрата этой случайной величины.

Моргана формулы или соотношения двойственности – Правило для записи выражения, соответствующего «отрицанию» функции.

Невозможное событие – это такое, которое не может наступить в условиях данного эксперимента, т. е. это событие имеет пустое множество благоприятствующих исходов.

Независимые сОбытия A и B – событие А происходит независимо от того, происходит событие В или нет.

Несовместные события A и B – не могут происходить одновременно.

Нормальное или гауссовское распределение – случайная величина ξ имеет плотность распределения вероятностей при всех X

.

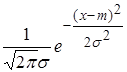- хи-квадрат (Пирсона) – Проверка гипотезы о совпадении дисперсий.

Относительная частота События A – Показывает долю опытов, в которых наступило событие A при N экспериментах.

Оценка интервальная – Доверительный интервал:

- несмещенная – Математическое ожидание случайной величины в этом случае равно оцениваемому параметру;

- точечная – Произвольная функция элементов выборки, когда параметр неизвестен.

Ошибка второго рода – событие, состоящее в том, что гипотеза принимается, когда на самом деле она неверна.

Ошибка первого рода – Событие, состоящее в том, что гипотеза отвергается, когда на самом деле она верна.

Показательное распределение с параметром – Это такое распределение, плотность вероятности которого задается равенством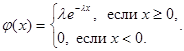

Произведение или пересечение Множеств A и B – множество, состоящее из всех общих элементов этих множеств.

Пространство Элементарных событий – множество всех исходов данного эксперимента.

Противоположное Событие – это событие, которое происходит в том случае, если не происходит событие А.

Пустое Множество – множество, не содержащее элементов.

Равномерное распределение - Случайная величина ξ на промежутке [A,B] Имеет постоянную Плотность распределения вероятностей.

Размещение из N элементов По K Элементов – Упорядоченные выборки объема K без возвращения элементов.

Разность множеств A и B – множество, состоящее из всех элементов множества A, которые не содержатся в множестве B.

Ряд распределения – статистический ряд, записанный в виде таблицы.

Случайная величина – Функция F, которая каждому элементарному событию w ставит в соответствие число ¦(w).

Событие – некоторое высказывание о результатах рассматриваемого эксперимента.

Сочетание из N Элементов по K элементов - неупорядоченные выборки объема K без возвращения элементов.

Стандартное или средне-квадратическое отклонение - Квадратный корень из дисперсии.

Статистика – Результат наблюдения над случайной величиной.

Статистический ряд – Последовательность различных значений, расположенных в возрастающем порядке, с указанием относительных частот.

Сумма или объединение множеств A и B – Множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.

Уровень значимости статистического критерия – Величина, определяющая степень достоверности вычислений.

Условие нормировки – Площадь криволинейной трапеции под всей кривой распределения равна 1.

Условная вероятность – вероятность события A при условии, что событие B Произошло.

Функция Лапласа - функция распределения стандартного нормального закона.

Функция распределения F(X) случайной величины X - Вероятность того, что случайная величина примет значение, меньшее заданного Х.

Частный случай – Если при каждом осуществлении события A происходит и событие B, То говорят, что событие A влечет событие B.

Частота события A – число экспериментов Mn(A), в которых наступило событие A.

Элементарные события – исходы (результаты) эксперимента.

Эмпирическая функция распределения – относительная частота события, заключающегося в том, что случайная величина примет значение, меньшее чем заданное число.

< Предыдущая		Следующая >