5.3. Элементы математической статистики
Перед тем как приступить к решению второй половины третьей задачи, следует изучить такие понятия, как: выборка, случайные числа; случайные числа распределенные по определенному закону; эмпирические (экспериментальные) ряд и функция распределения; оценки параметров распределения; метод жребия моделирования дискретной величины; критерии Пирсона оценки достоверности гипотезы; доверительные вероятности и интервалы. Следует разобрать примеры 5.10, 5.11.
Коротко рассмотрим, в чем заключается метод жребия моделирования дискретной случайной величины. Пусть событие А может произойти с вероятностью Р, и пусть очередное значение случайного числа – Ri (случайное число – значение непрерывной случайной величины, равномерно распределенной в интервале [0,1]). Если Ri £ Р , то оно принадлежит интервалу 
, поэтому считаем, что событие А наступило. Если Ri>Р, то считается, что событие А не наступило.
Поскольку значения случайной величины ни что иное как случайные события, процедура моделирования дискретной случайной величины с заданным законом распределения аналогична моделированию случайного события.
Пусть дискретная случайная величина задана теоретическим рядом распределения.
|
H |
Х1 |
Х2 |
Х3 |
… |
ХN |
|
Pi |
Р(Х1) |
Р(Х2) |
Р(Х3) |
… |
Р(ХN) |
Присваиваем случайной величине h значение Х1, если значение случайного числа Ri£P(Х1), значение Х2, если P(Х1)<Ri£P(Х1)+P(Х2), т. е. в общем случае, если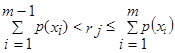 
, то случайной величине h присваивается значение ХM.
Пример 5.10. Дискретная случайная величина задана рядом распределения, приведенным в табл. 5.3.
Таблица 5.3
|
ХI |
0 |
5 |
10 |
15 |
|
Pi |
0.6189 |
0.0896 |
0.2547 |
0.0368 |
1. Построить модель этой случайной величины для партии из 25 приборов (методом жребия получить её 25 значений); найти экспериментальные ряд и функцию распределения, построить их графики.
2. Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
3. С помощью критерия Пирсона оценить соответствие экспериментального распределения теоретическому при уровнях значимости a1=0.01, a2= 0.05.
Решение. 1. Приступим к построению модели данной случайной величины. Этот процесс будем осуществлять методом жребия с помощью случайных чисел Rj, т. е. значений случайной величины равномерно распределенной в интервале 
. Эти значения приведены в табл. Д Приложения. Моделируемые значения случайной величины обозначим Zj (J = 1, 2, …, 25). Заметим, что каждое из них следует рассматривать как случайную величину.
Для рассматриваемой случайной величины правило моделирования заключается в том, чтобы определить какое значение будет принимать случайная величина в зависимости от попадания случайного числа в интервал.
H примет значение:
0, если Rj £ 0.6189,
5, если 0.6189< RJ£ 0.7085,
10, если 0.7085< Rj£ 0.9631,
15, если Ri> 0.9631.
Для удобства использования правило можно свести в табл. 5.4 или изобразить на рис. 5.7.
Таблица 5. 4
|
