4.1.3.Критерий согласия Пирсона
Предположим, что выполнено 
измерений некоторой случайной величины ξ : 
, ..., 
, (4.4)
И есть основания полагать, что результаты распределены нормально с плотностью вероятности
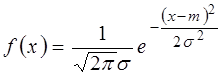. (4.5)
Параметры закона распределения 
и σ обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляют по следующим формулам:
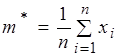, (4.6)
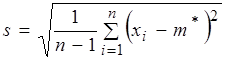. (4.7)
В качестве критерия проверки выдвинутой гипотезы примем критерий согласия Пирсона (критерий согласия “хи- квадрат”)
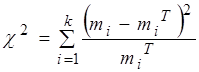, (4.8)
Где 
– число интервалов, на которые разбито выборочное распределение, 
- частоты эмпирического распределения; 
– частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются и 
, тем меньше значение χ2.
Доказано, что при 
закон распределения случайной величины (4.8) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с 
степенями свободы. Число степеней свободы определяется равенством 
, где 
- число частичных интервалов; 
– число параметров предполагаемого распределения, которые были оценены. Для нормального распределения оцениваются два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому 
.
В соответствии с процедурой проверки гипотезы следует вычислить наблюдаемое значение критерия. Чтобы вычислить частоты эмпирического распределения, весь интервал наблюдаемых значений делят на частичных интервалов (бинов) точками 
:
. (4.9)
определяют, подсчитав число измерений (4.4), которые попадают в 
- й интервал 
.
Используя теоретический закон распределения (4.5) можно рассчитать ожидаемое число Результатов измерений для каждого интервала 
. Вероятность того, что результат одного измерения попадает в интервал , равна
, (4.10)
Где 
– интегральный закон нормального распределения: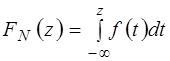 
. Учитывая, что функция распределения 
с параметрами и σ связана со стандартной нормальной функцией формулой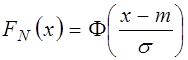 
, соотношение (4.10) можно записать в следующем виде:
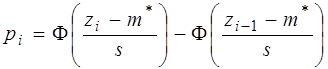. (4.11)
Поскольку проводится не одно, а измерений и эти измерения независимы, то их можно рассматривать как испытаний Бернулли, в которых “успехом” считается попадание результата измерения в интервал . Тогда числа 
вычисляются по формуле
(4.12)
(математическое ожидание числа “успехов” при испытаниях).
Для заданного уровня значимости по таблицам определяют критическое значение критерия. Сравнивая наблюдаемое и критическое значения критерия делают, вывод о соответствии экспериментальных данных предполагаемому закону распределения.
Пример 4.1. Проверить с помощью критерия χ2 при уровне значимости 0,05 гипотезу о том, что выборка объема 
, представленная интервальным вариационным рядом в таблице 4.4, извлечена из нормальной генеральной совокупности.
Таблица 4.4
|
Номер Интервала I |
Границы Интервала |
Частота
|
|
1 |
0 – 2 |
5 |
|
2 |
2 – 4 |
11 |
|
3 |
4 –6 |
17 |
|
4 |
6 – 8 |
10 |
|
5 |
8 – 10 |
7 |
Решение. 1. Сформулируем нулевую и альтернативную гипотезы: H0 – эмпирическое распределение соответствует нормальному; H1 - эмпирическое распределение не соответствует нормальному.
Для проверки нулевой гипотезы необходимо рассчитать наблюдаемое значение критерия χ2набл по формуле (4.8) и сравнить его с критическим значением χ2кр.
2. Определим параметры предполагаемого (теоретического) нормального закона распределения.
Найдем середины интервалов 
и относительные частоты 
. Получим следующие значения:
|
|
1 |
3 |
5 |
6 |
7 |
|
|
|
|
|
|
|
Оценку математического ожидания найдем по формуле (4.1):
.
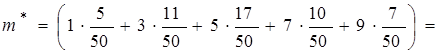
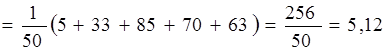Оценки дисперсии и стандартного отклонения вычислим по формулам (4.2) и (4.3):
;
.
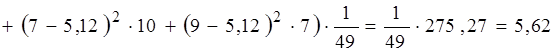3. Выполним расчет теоретических частот по формуле (4.12). Для вычисления вероятностей 
по формуле (4.11) воспользуемся таблицей В Приложения со значениями нормальной стандартной функции распределения. При этом наименьшее значение, т. е. 
, полагаем равным 
, а наибольшее, т. е. 
, полагаем равным 
. Последовательно находим для интервала (-∞, 2)
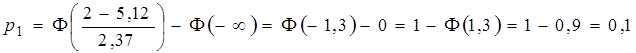и 
;
Для интервала 
находим
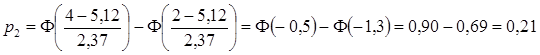
и 
;
Для интервала (4,6) соответственно :
;
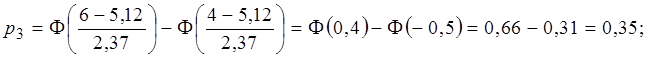
Для интервала (6,8):
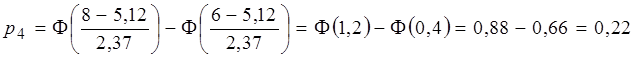
И 
;
Для интервала 
вычислим
;
.
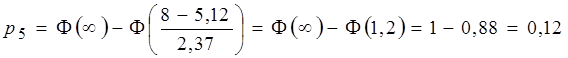4. По формуле (4.8) найдем значение 
:
.
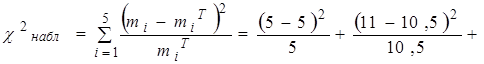
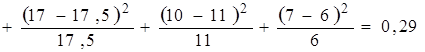5. По таблице квантилей распределения χ2 (см. таблицу С Приложения) с числом степеней свободы 
находим, что χ2кр = 6,0 для 
.
Поскольку 
(
), то можно считать, что гипотеза о нормальном распределении генеральной совокупности не противоречит опытным данным.
Порядок выполнения лабораторной работы
В данной лабораторной работе задания 1 и 2 представляют собой контрольный пример, решение которого приводится ниже. Задания 3 и 4 составляют индивидуальное задание.
Задание 1. Для выборки из 40 значений случайной величины ξ, полученной в задании 1 работы 1, оценить близость эмпирического распределения к нормальному распределению:
А) построить интервальный вариационный ряд и гистограмму частот;
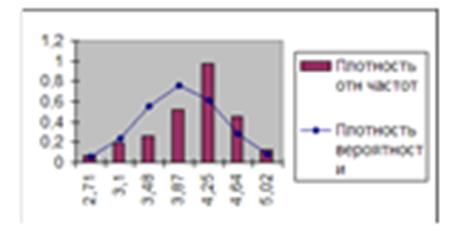
Б) построить на одном графике гистограмму относительных частот и график плотности нормального распределения.
Задание 2. При уровне значимостит 0,05 проверить гипотезу о нормальном распределении генеральной совокупности с использованием χ2 - критерия как критерия согласия.
Задание 3. Для выборки нормальной случайной величины, смоделированной в задании 3 работы 1, построить, на выбор, либо гистограмму частот, либо гистограмму относительных частот.
Задание 4. Пользуясь критерием Пирсона при уровне значимости 0,01 проверить, согласуется ли с нормальным распределением статистическое распределение из задания 3 работы 1.
Выполнение задания 1.
1. Подготовьте рабочий лист в EXCEL. Для этого выполните следующее:
· перейдите на новый лист и введите в ячейку B1 название таблицы ПОСТРОЕНИЕ ГИСТОГРАММЫ;
· назовите ярлык листа Гистограмма;
· разместите в ячейках A5:B24 выборку, которая была получена при выполнении задания 1.1 лабораторной работы 1 (40 значений нормальной случайной величины с параметрами 
и σ=0,5 ), либо выполнив копирование значений с листа Оценки, либо повторив процедуру моделирования выборки заданного закона распределения.
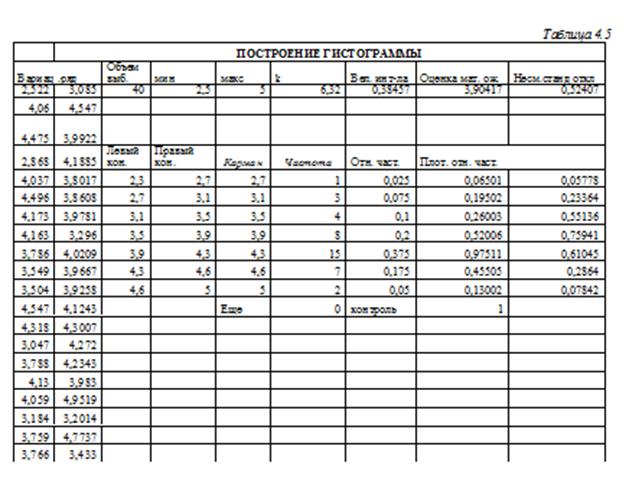
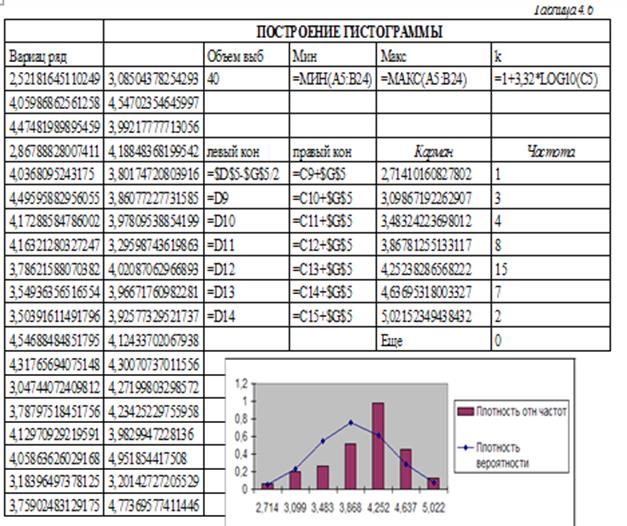
Создаваемая электронная таблица представлена в таблице 4.5 в режиме вычислений и в таблице 4.6 в режиме формул.
2. Для построения интервального вариационного ряда выполните следующие действия:
2.1. Произведите расчет длины частичных интервалов в ячейках C5:G5 по указанным в ячейках формулам и комментариям так, как указано ниже.
Ячейка Значение Ячейка Значение
C5 40 C4 объем выб.
D5 =МИН(A5:B24) D4 минимум
E5 =МАКС(A5:B24) E4 максимум
F5 =1+3,32*LOG10(C5) F4 k
G5 =(E5-D5)/F5 G4 вел. инт-ла
H5 =СРЗНАЧ(A5:B24) H4 оценка мат. ож.
I5 =СТАНДОТКЛОН(A5:B24) I4 несм. станд. откл.
2.2. Разместите массив значений границ интервалов в ячейках C9:D15 (в столбце С – значения левых границ, в столбце D – значения правых границ).
Выполните это так:
· для определения левой границы первого частичного промежутка введите в ячейку С9 формулу - =$D$5-$G$5/2;
· для определения правой границы введите в ячейку D9 формулу C9+$G$5;
· поскольку левая граница последующего частичного промежутка совпадает с правой границей предыдущего введите в ячейку С10 формулу - =D9;
· перенесите автозаполнением формулу из ячейки С10 на диапазон С11:C15, а формулу из D9 – в ячейки D10:D15;
· в ячейку С8 введите текст Левый кон, в ячейку D8 – Правый кон.
3. Для построения гистограммы частот воспользуемся инструментом анализа Гистограмма. Выполните команду Сервис – Анализ данных – Гистограмма. В окне “Гистограмма” задайте параметры;
· введите в поле Входной интервал $A$5:$B$24, в поле Интервал карманов – $D$9:$D$15, в Выходной интервал – $E$8;
· установите флажок Вывод графика;
· нажмите OK.
На экране появятся выходная таблица и гистограмма. В левом столбце таблицы размещен Карман – так в MS Excel называется набор граничных значений частичных интервалов. Правый столбец содержит вычисленные значения частот.
Поместите полученную диаграмму (выделите и перетащите) так, чтобы левый верхний конец находился в ячейке J8.
4. Подготовим исходные данные для построения гистограммы относительных частот и графика плотности вероятности.
4.1. Расчет относительных частот произведите в ячейках G9:G15, для этого введите в ячейку G9 формулу =F9/$C$5 и перенесите ее на диапазон G10:G15.
4.2. При построении гистограммы используются значения плотности относительных частот. Выполните расчет этих значений в ячейках H9:H15. Введите в ячейку H9 формулу =G9/$G$5 и скопируйте ее в ячейки H10:H15. Озаглавьте столбцы: введите в G8 текст Отн. част., в H8 – Плот. отн. част.
4.3. Сформируйте в ячейках I9:I15 массив значений плотности вероятности, по которым будет построен график. Указанные значения вычислите с использованием функции НОРМРАСП в граничных точках частичных интервалов, размещенных в ячейках D9:D15. Введите в I9 формулу
=НОРМРАСП(D9;$H$5;$I$5;0)
И перенесите ее на диапазон I10:I15.
5. Как отмечалось выше, площадь гистограммы относительных частот численно равна единице. Введите для контроля правильности вычислений в ячейку G16 текст Контроль, а в ячейку H16 – формулу =СУММ(H9:H15)*$G$5.
6. Для построения гистограммы и графика выполните следующие действия:
· выделите ячейки H9:I15, в которых размещены данные;
· нажмите кнопку Мастер диаграмм, откроется окно диалога;
· выберите вкладку “Нестандартные” и вид графика График! гистограмма, нажмите кнопку Далее;
· на втором шаге построения диаграммы выберите вкладку “Ряд”. Измените текст легенды (условного обозначения для рядов данных): в разделе Ряд выделите Ряд 1, перейдите в поле Имя и введите текст Плотность вероятности, затем выделите Ряд 2 и в поле Имя Наберите Плотность отн. частот;
· введите в поле “Подписи оси Х” диапазон D9:D15 и нажмите кнопку Далее;
· оформление гистограммы на третьем шаге можно опустить (либо выполните по своему желанию);
· на четвертом шаге задайте место размещения гистограммы –Имеющийся лист И нажмите OK.
Выполнение задания 2
1. Подготовьте рабочий лист. Для этого выполните следующие действия:
· перейдите на новый лист и введите в ячейку С1 название таблицы ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА;
· назовите ярлык листа Крит Пирсона;
· занесите в ячейку E2 значение заданного уровня значимости 0,05, а в С2 - Уровень значимости;
· перенесите содержимое столбцов A, B, C, D, а также четвертой и пятой строк с листа Гистограмма На лист Крит Пирсона.
Создаваемая электронная таблица представлена в таблице 4.7 в режиме формул и в таблице 4.8 в режиме вычислений.
Чтобы вычислить наблюдаемое значение критерия по формуле (4.7), для каждого частичного интервала необходимо найти значения эмпирической и теоретической частот.
2. Частоту появления значений выборки в построенных частичных интервалах (эмпирическую частоту) вычислите с помощью функции ЧАСТОТА, которая возвращает распределение частот в виде вертикального массива. Эта функция подсчитывает для данного множества значений и данного множества карманов (интервалов, в математическом смысле), сколько исходных значений попадает в каждый интервал. Выполните следующие действия:
· выделите ячейки E9:E15, в которые будет введена функция ЧАСТОТА (данная функция возвращает массив, поэтому она должна задаваться в качестве формулы массива);
· нажмите кнопку Вставка функции;
· в открывшемся окне диалога “Мастер функций” выберите функцию ЧАСТОТА из категории Статистические и нажмите кнопку OK;
· укажите в поле Массив данных диапазон $A$5:$B$24, в поле Двоичный массив – $D$9:$D$15 (массив верхних границ интервалов);
· не выходя из строки формул, одновременно нажмите клавиши Ctrl+Shift+Enter;
· введите в ячейку E7 текст Эмп. частота, в D16 – Число бинов, а в E16 – формулу для подсчета числа бинов
=СЧЕТ(E9:E15).
3. Расчет теоретической частоты по формулам (4.10) и (4.12) произведите в ячейках F9:H15. Выполните следующее:
· определите значения интегральной функции распределения на правом конце для каждого частичного промежутка, для чего введите в ячейку F9 формулу =НОРМРАСП(D9;$H$5;$I$5;1)
· и перенесите ее автозаполнением на диапазон F10:F14 (в ячейку F15 введите 1, поскольку 
);
· вычислите вероятность того, что результат одного измерения попадет в частичный интервал, для чего введите в ячейку G9 формулу: =F9-F8
И скопируйте ее на диапазон G10:G15;
· сосчитайте теоретические частоты, введя в ячейку H9 формулу:
=$C$5*G9
и автозаполнением перенесите ее на диапазон H10:H15;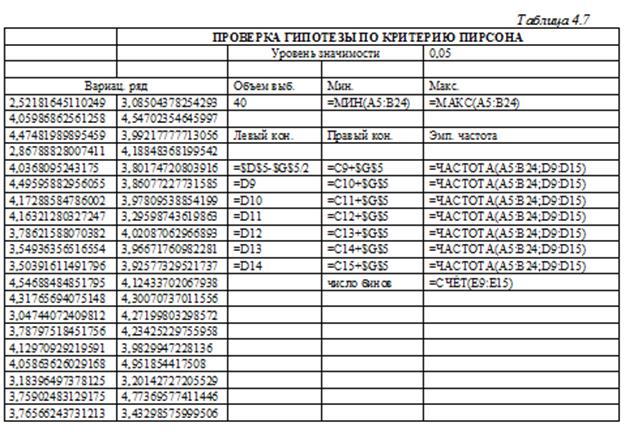 
Продолжение таблицы 4.7
|
|
| ||
|
K |
Вел инт-ла |
Оценка мат ож |
Несм станд откл |
|
=1+3,32*LOG10(C5) |
=(E5-D5)/F5 |
=СРЗНАЧ(A5:B24) |
=СТАНДОТКЛОН(A5:B24) |
|
Ф р на пр конце |
Вер |
Теор частота | |
|
| |||
|
=НОРМРАСП(D9;$H$5;$I$5;1) |
=F9-F8 |
=$C$5*G9 |
=(E9-H9)^2/H9 |
|
=НОРМРАСП(D10;$H$5;$I$5;1) |
=F10-F9 |
=$C$5*G10 |
=(E10-H10)^2/H10 |
|
=НОРМРАСП(D11;$H$5;$I$5;1) |
=F11-F10 |
=$C$5*G11 |
=(E11-H11)^2/H11 |
|
=НОРМРАСП(D12;$H$5;$I$5;1) |
=F12-F11 |
=$C$5*G12 |
=(E12-H12)^2/H12 |
|
=НОРМРАСП(D13;$H$5;$I$5;1) |
=F13-F12 |
=$C$5*G13 |
=(E13-H13)^2/H13 |
|
=НОРМРАСП(D14;$H$5;$I$5;1) |
=F14-F13 |
=$C$5*G14 |
=(E14-H14)^2/H14 |
|
1 |
=F15-F14 |
=$C$5*G15 |
=(E15-H15)^2/H15 |
|
Набл зн критерия |
=СУММ(I9:I15) | ||
|
Крит зн критерия |
=ХИ2ОБР($E$2;$E$16-3) | ||
Таблица 4.8
|
|
ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА | |||||||
|
Уровень значимости |
0,05 | |||||||
|
Вариац. ряд |
Объем выб. |
Мин. |
Макс |
K |
Вел. инт-ла |
Оценка мат ожидания |
Несм. станд. откл. | |
|
2,522 |
3,08504 |
40 |
2,52182 |
4,951854 |
6,318839171 |
0,3845703 |
3,904166 |
0,5240692 |
|
4,06 |
4,54702 | |||||||
|
4,475 |
3,99218 |
Левый кон. |
Правый кон. |
Эмп. частота |
Ф. р. на пр..конце |
Вер. |
Теор. частота | |
|
2,868 |
4,18848 |
|
| |||||
|
4,037 |
3,80175 |
2,3295 |
2,7141 |
1 |
0,011579055 |
0,0115791 |
0,463162 |
0,622233 |
|
4,496 |
3,86077 |
2,7141 |
3,09867 |
3 |
0,062146626 |
0,0505676 |
2,022703 |
0,4721948 |
|
4,173 |
3,9781 |
3,0987 |
3,48324 |
4 |
0,210934098 |
0,1487875 |
5,951499 |
0,6398973 |
|
4,163 |
3,29599 |
3,4832 |
3,86781 |
8 |
0,472348174 |
0,2614141 |
10,45656 |
0,577121 |
|
3,786 |
4,02087 |
3,8678 |
4,25238 |
15 |
0,746798016 |
0,2744498 |
10,97799 |
1,473542 |
|
3,549 |
3,96672 |
4,2524 |
4,63695 |
7 |
0,918983001 |
0,172185 |
6,887399 |
0,0018409 |
|
3,504 |
3,92577 |
4,637 |
5,02152 |
2 |
1 |
0,081017 |
3,24068 |
0,4749888 |
|
4,547 |
4,12434 |
Число бинов |
7 |
Набл. зн. .критерия |
4,2618178 | |||
|
4,318 |
4,30071 |
Крит. зн. критерия |
9,487729 | |||||
|
3,047 |
4,272 | |||||||
|
3,788 |
4,23425 | |||||||
|
4,13 |
3,98299 | |||||||
|
4,059 |
4,95185 | |||||||
|
3,184 |
3,20143 | |||||||
|
3,759 |
4,7737 | |||||||
|
3,766 |
3,43299 |
- поясните полученные результаты, для этого в ячейку F7 введите текст Ф. р. на пр. конце, в ячейку G7 – Вер., а в H7 – Теор. частота.
4. Вычислите слагаемые критерия Пирсона, для чего введите в ячейку I9 формулу
=(E9-H9)^2/H9
И автозаполнением перенесите эту формулу в ячейки I10:I15.
5. Наблюдаемое значение критерия вычислите по формуле (4.6) в ячейке I16, для чего введите формулу =СУММ(I9:I15).
6. Критическое значение критерия “хи-квадрат” для уровня значимости 0,95 и числа степеней свободы 
выведите в ячейке I17, набрав формулу
=ХИ2ОБР($E$2;$E$16-3).
Функция ХИ2ОБР возвращает обратную функцию для χ2-распределения.
В ячейку H16 введите текст Набл. зн. критерия, а в H17 – Крит. зн. критерия.
Так как наблюдаемое значение критерия, равное 4,26, меньше критического значения, равного 9,49, то гипотезу о нормальном распределении генеральной совокупности не отвергаем. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, смоделированные значения случайной величины согласуются с гипотезой о распределении случайной величины с заданным законом распределения.
Подготовить отчет:
1. Название работы и задание.
2. По две распечатки таблиц, созданных при выполнении заданий 3 и 4 (одна распечатка содержит результаты вычислений, другая – сами формулы).
3. Выводы по результатам выполнения задания 4.
| < Предыдущая | Следующая > |
|---|
