2.2.5. Распределение Пуассона

Определение. Случайная величина x распределена По закону Пуассона С параметром распределения L>0, если она принимает значения M= 0,1, 2,…

с вероятностями

Pm= P (x =M ) = 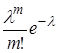, M= 0,1,2,… (2.39)

Пример 2.10. Рассмотрим случайную величину x, равную числу покупателей, посетивших супермаркет в промежутке времени от T0 до T. Появление покупателей - случайные события и происходят в случайные моменты времени.

Сделаем следующие предположения.

1. Вероятность появления одного покупателя за малый промежуток времени пропорциональна , т. е. равна

а > 0,

Где - бесконечно малая величина при .

2. Если за малый промежуток времени уже произошло одно событие, то условная вероятность появления в этом же промежутке другого события стремится к 0 при

3. События на непересекающихся промежутках времени являются независимыми случайными величинами.

В этих условиях можно доказать, что число покупателей, посетивших супермаркет в промежутке времени от T0 до T распределено по закону Пуассона с параметром

Вопросы для самопроверки

1. Как вычислить математическое ожидание и дисперсию:

А) для дискретной случайной величины?

Б) для непрерывной случайной величины?

2. Как найти плотность вероятности для случайной величины, имеющей равномерное распределение?

3. Что такое нормально распределенная случайная величина?

4. Какие другие законы распределения известны?

< Предыдущая		Следующая >