1.3.1. Последовательность независимых испытаний (схема Бернулли)
Предположим, что некоторый эксперимент можно проводить неоднократно при одних и тех же условиях. Пусть этот опыт производится N раз, т. е. проводится последовательность из N испытаний.
Определение. Последовательность N Испытаний называют Взаимно независимой, если любое событие, связанное с данным испытанием, не зависит от любых событий, относящихся к остальным испытаниям.
Допустим, что некоторое событие A может произойти с вероятностью P в результате одного испытания или не произойти с вероятностью Q=1-P.
Определение. Последовательность из N Испытаний образует схему Бернулли, если выполняются следующие условия:
1) последовательность N испытаний взаимно независима,
2) вероятность события A не изменяется от испытания к испытанию и не зависит от результата в других испытаниях.
Событие A называют “ успехом” испытания, а противоположное событие ![]() - “неудачей”. Рассмотрим событие
- “неудачей”. Рассмотрим событие
![]() ={ в N испытаниях произошло ровно M “успехов”}.
={ в N испытаниях произошло ровно M “успехов”}.
Для вычисления вероятности этого события справедлива формула Бернулли
P(![]() ) =
) = ![]() , M = 1, 2, …, N , (1.6)
, M = 1, 2, …, N , (1.6)
где ![]() - число сочетаний из N элементов по M :
- число сочетаний из N элементов по M :
![]() =
= ![]() =
= ![]() .
.
Пример 1.16. Три раза подбрасывают кубик. Найти:
а) вероятность того, что 6 очков выпадет два раза;
б) вероятность того, что число шестерок не появится более двух раз.
Решение. “Успехом” испытания будем считать выпадение на кубике грани с изображением 6 очков.
А) Общее число испытаний – N =3, число “успехов” – M = 2. Вероятность “успеха” - P=![]() , а вероятность “неудачи” - Q= 1 -
, а вероятность “неудачи” - Q= 1 - ![]() =
= ![]() . Тогда по формуле Бернулли вероятность того, что результате трехразового бросания кубика два раза выпадет сторона с шестью очками, будет равна
. Тогда по формуле Бернулли вероятность того, что результате трехразового бросания кубика два раза выпадет сторона с шестью очками, будет равна
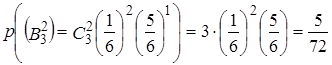 .
.
Б) Обозначим через А событие, которое заключается в том, что грань с числом очков 6 появится не более двух раз. Тогда событие можно представить в виде Суммы трех несовместных событий А= ![]() ,
,
Где В30 – событие, когда интересующая грань ни разу не появится,
В31 - событие, когда интересующая грань появится один раз,
В32 - событие, когда интересующая грань появится два раза.
По формуле Бернулли (1.6) найдем
P(А) = р (![]() ) = P(
) = P(![]() )=
)=![]() +
+![]() +
+![]() =
=
=![]() .
.
| < Предыдущая | Следующая > |
|---|