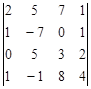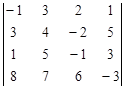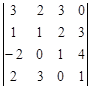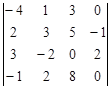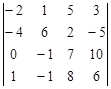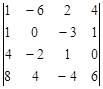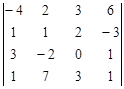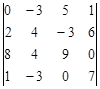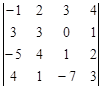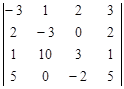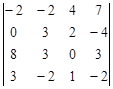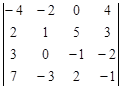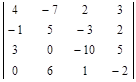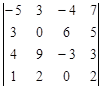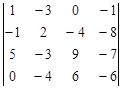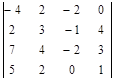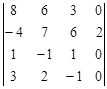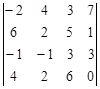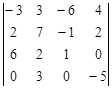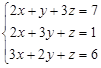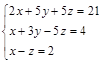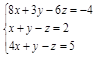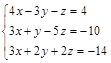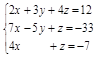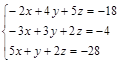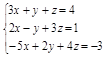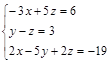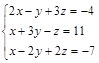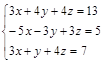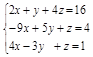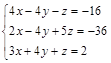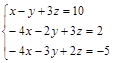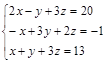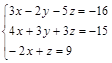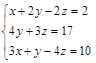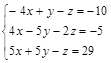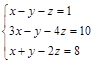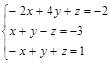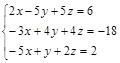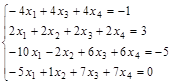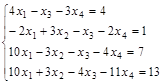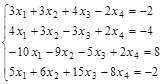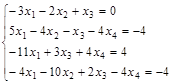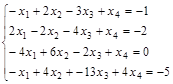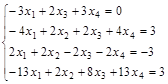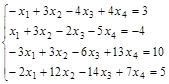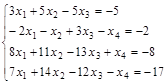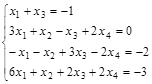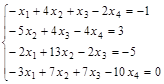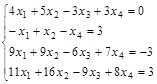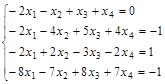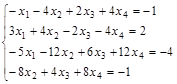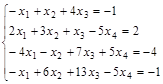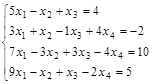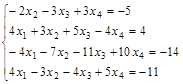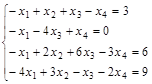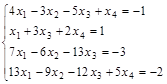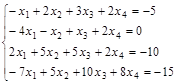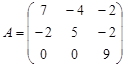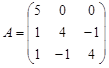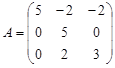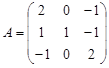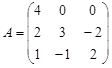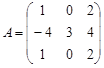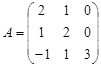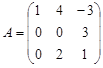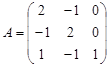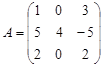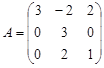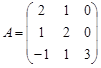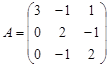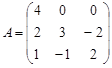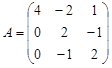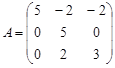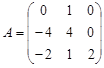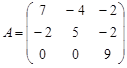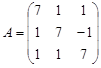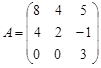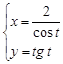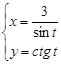23. Индивидуальные задания

Задание№1. Вычислить матрицу C, если даны матрицы A и B.

Вариант 1.

C = A∙B- 2AT

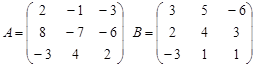
Вариант 2.

C = – 2BT + A∙B

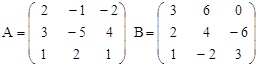
Вариант 3.

C = 4A – (A∙B)T

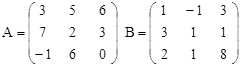
Вариант 4.

C = 3A + (A∙B)T

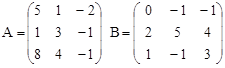
Вариант 5.

C = 2A+ (A∙B)T

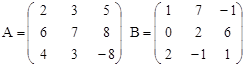
Вариант 6.

C = 3 BT - A∙B

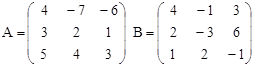
Вариант 7.

C = -B + (A∙B)T

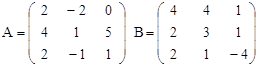
Вариант 8.

C = -A + (A∙B)T

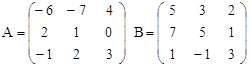
Вариант 9.

C = 2 (A∙B)T-A

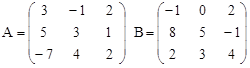
Вариант 10.

C = - (A∙B)T+3A

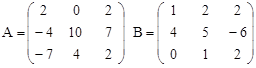
Вариант 11.

C = (A∙B)T-2B

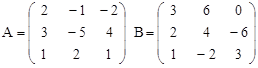
Вариант 12.

C = (A∙B)T-3B

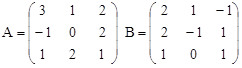
Вариант 13.

C = – 2B + (A∙B)T

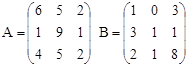
Вариант 14.

C = -2A + (A∙B)T

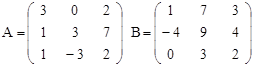
Вариант 15.

C = -3A – (A∙B)T

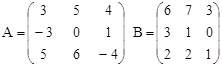
Вариант 16.

C = (A∙B)Т – B

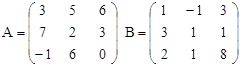
Вариант 17.

C = 3A – 4B + (A∙B)T

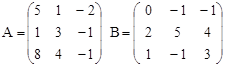
Вариант 18.

C = 4A – (A∙B)T

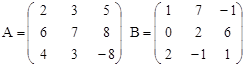
Вариант 19.

C = – 3B + (A∙B)T

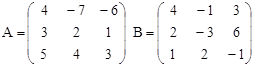
Вариант 20.

C = 2AТ + A∙B

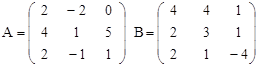
Задание №2. Вычислить определитель

А) Разложением по элементам какой-либо строки или столбца

Б) Сведением к треугольному виду.

Вар.		Вар.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №3. Найти ранг матрицы.

Вариант 1.

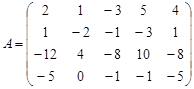
Вариант 2.

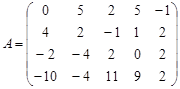
Вариант 3.

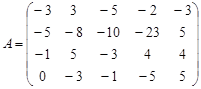
Вариант 4.

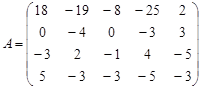
Вариант 5.

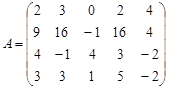
Вариант 6.

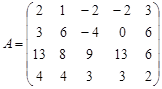
Вариант 7.

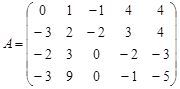
Вариант 8.

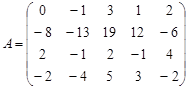
Вариант 9.

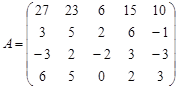
Вариант 10.

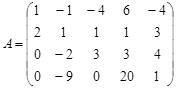
Вариант 11.

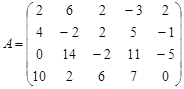
Вариант 12.

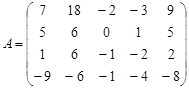
Вариант 13.

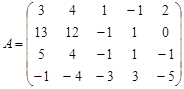
Вариант 14.

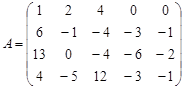
Вариант 15.

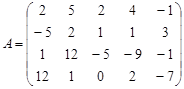
Вариант 16.

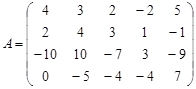
Вариант 17.

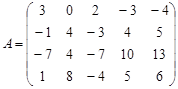
Вариант 18.

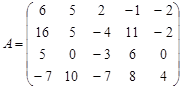
Вариант 19.

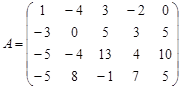
Вариант 20.

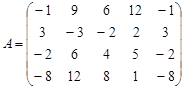
Задание№4. Решить систему уравнений

А) Методом обратной матрицы

Б) Методом Крамера

В) Методом Гаусса

Вар.		Вар.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание№5. Найти общее и два частных решения системы уравнений.

Вар.		Вар.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №6. Найти собственные числа и собственные векторы матрицы.

Вар.		Вар.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №7. Определить, при каких значениях квадратичная форма положительно определена.

Вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание №8. Показать, что векторы образуют базис в пространстве и разложить вектор по этому базису.

Вар
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание №9. Даны координаты вершин пирамиды A1A2A3A4. Найти:

Угол между ребрами A1A2 и A1A3; Площадь сечения, проходящего через середину ребра A1A4 и вершины пирамиды A2 и A3 Объем пирамиды Уравнение прямой A1A4; Уравнение плоскости A1A2A3; Угол между прямой A1A4 и плоскостью A1A2A3.

Вар.	A1	A2	A3	A4
1	(–4; –3; 0)	(0; 4; 0)	(2; 2; –5)	(–2; 7; 6)
2	(0; 6; 1)	(6; –2; 4)	(1; 7; 3)	(–6; 2; –6)
3	(5; 2; –4)	(–5; –2; 3)	(–7; 8; 4)	(1; –6; 2)
4	(–3; –1; –3)	(–6; –5; –1)	(5; 8; –5)	(–7; –7; –6)
5	(1; –7; 0)	(–2; –3; 3)	(–1; 0; –2)	(–7; 3; 7)
6	(–2; –6; –1)	(0; –1; –6)	(7; 7; –7)	(–2; –7; 7)
7	(4; –2; –1)	(7; 0; 7)	(5; 6; 4)	(–5; –1; –1)
8	(2; 1; 6)	(–7; 1; 4)	(3; –2; –1)	(2; –4; 7)
9	(1; 1; –6)	(–3; –7; –2)	(8; –5; 7)	(–1; 1; –3)
10	(1; 4; 2)	(–3; –7; –1)	(–3; 7; –4)	(–4; –7; –6)
11	(6; –2; 0)	(–4; 3; 6)	(3; –1; –4)	(–4; 6; 0)
12	(3; 3; –5)	(0; –3; 6)	(1; –6; –2)	(–1; 7; –1)
13	(–6; 1; 5)	(8; –3; –4)	(–3; 2; –7)	(–7; –5; 5)
14	(0; –3; 6)	(7; –1; –2)	(–7; –2; 6)	(–4; 1; 3)
15	(3; –7; 0)	(6; 3; 5)	(–7; –2; 4)	(5; 8; –4)
16	(–6; 0; 5)	(1; –6; –4)	(–1; –5; –2)	(–3; –2; 3)
17	(–5; 4; 6)	(–2; –3; 6)	(7; –3; 1)	(–5; –2; 0)
18	(2; 0; –5)	(–1; –4; 1)	(–5; 1; –1)	(5; 3; 3)
19	(4; 0; 3)	(6; 3; 3)	(–7; –5; 1)	(0; 0; –4)
20	(5; 8; 6)	(1; –1; –7)	(0; 0; –2)	(7; 6; 4)

Задание №10. В вершинах пирамиды (из задания 9) сосредоточены массы соответственно. Найти координаты центра тяжести системы точек.

Задание №11.

Даны три силы , приложенные к точке A. Вычислить:

1.Работу, которую производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается в точку B;

2.Момент равнодействующей этих сил относительно точки B.

Вар.				A	B
1	(3; –2; 4)	(–4; 3; –3)	(3; 4; 2)	(1; –4; 3)	(4; 0; –2)
2	(3; –4; 2)	(2; 3; –5)	(–3; –2; 4)	(5; 3; –7)	(4; –1; –4)
3	(7; 3; –4)	(9; –4; 2)	(–6; 1; 4)	(–7; 2; 5)	(4; –2; 11)
4	(9; –4; 4)	(–4; 6; –3)	(3; 4; 2)	(5; –4; 3)	(4; –5; 9)
5	(5; 5; –6)	(7; –6; 6)	(–4; 3; 4)	(–9; 4; 7)	(8; –1; 7)
6	(9; –3; 4)	(5; 6; –2)	(–4; –2; 7)	(–5; 4; –2)	(4; 6; –5)
7	(5; –3; 1)	(4; 2; –6)	(–5; –3; 7)	(–5; 3; 7)	(3; 8; –5)
8	(–5; 8; 4)	(6; –7; 3)	(3; 1; –5)	(2; –4; 7)	(0; 7; 4)
9	(7; –5; 2)	(3; 4; –8)	(–2; –4; 3)	(–3; 2; 0)	(6; 4; –3)
10	(5; –2; 3)	(4; 5; –3)	(–1; –3; 6)	(7; 1; –5)	(2; –3; –6)
11	(3; –5; 4)	(5; 6; –3)	(–7; –1; 8)	(–3; 5; 9)	(5; 6; –3)
12	(–10; 6; 5)	(4; –9; 7)	(5; 3; –3)	(4; –5; 9)	(4; 7; –5)
13	(7; –6; 2)	(–6; 2; –1)	(1; 6; 4)	(3; –6; 1)	(6; –2; 7)
14	(4; –2; 3)	(–2; 5; 6)	(7; 3; –1)	(–3; –2; 5)	(9; –5; 4)
15	(2; –1; –3)	(3; 2; –1)	(–4; 1; 3)	(–1; 4; –2)	(2; 3; –1)
16	(3; –4; 2)	(2; 3; –5)	(–3; –2; 4)	(5; 3; –7)	(4; –1; –4)
17	(4; –2; –5)	(5; 1; –3)	(–6; 2; 5)	(–3; 2; –6)	(4; 5; –3)
18	(7; 3; –4)	(3; –2; 2)	(–5; 4; 3)	(–5; 0; 4)	(4; –3; 5)
19	(6; –4; 5)	(–4; 7; 8)	(5; 1; –3)	(–5; –4; 2)	(7; –3; 6)
20	(2; –2; 3)	(–1; 6; –1)	(2; –6; –7)	(2; –3; 5)	(3; –2; –1)

Задание №12.Дано уравнение линии в полярной системе координат. Найти уравнение этой линии в виде и построить ее.

Вар		Вар
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №13. Даны параметрические уравнения линий, исключив параметр T, найти уравнение этой линии в виде . Сделать схематический рисунок.

Вар		Вар
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №14. Определить тип поверхности второго порядка, заданной уравнением и проходящей через три данные точки.

Вар.	A1	A2	A3
1	(–4; –3; 0)	(–2; 5; 1)	(2; 2; 0)
2	(–3; 3; 1)	(0; –2; 4)	(1; 2; 3)
3	(3; 2; 1)	(–2; 1; 4)	(4; -3; 2)
4	(3; –1; –3)	(–2; 5; –1)	(5; 0; 4)
5	(–2; 3; 0)	(0; 2; 3)	(–1; 0; 2)
6	(–2; –3; 1)	(–1; 1; 0)	(0; -2; 3)
7	(4; –2; –1)	(–5; –1; 0)	(0; 6; 4)
8	(2; 1; 6)	(0; 1; 4)	(3; –2; –1)
9	(1; 1; –6)	(–3; 0; –1)	(2; 2; 0)
10	(1; 4; 2)	(–3; 0; –1)	(4; 4; –3)
11	(6; –2; 0)	(–4; 3; 6)	(3; –1; –4)
12	(3; 3; –5)	(–1; 2; –1)	(1; –6; –2)
13	(–2; 1; 1)	(3; –3; –4)	(–1; 2; 0)
14	(–4; 1; 3)	(1; –1; –2)	(0; –2; 5)
15	(5; 1; –4)	(0; 3; 5)	(–1; –2; 4)
16	(–3; –2; 3)	(1; –2; –4)	(–1; 0; –2)
17	(–5; 4; 1)	(–2; –3; 2)	(0; –3; 1)
18	(5; 3; 3)	(–1; –4; 1)	(–2; 1; –1)
19	(4; 0; 3)	(2; 3; 3)	(1; –5; 1)
20	(5; 0; 6)	(1; –1; 2)	(1; 2; 4)

< Предыдущая		Следующая >