14. Приложения векторной алгебры к решению физических задач

Векторная запись многих уравнений физики более полно отражает соответствующие процессы и является более простой и компактной.

Если в результате движения вдоль какой-то кривой материальная точка переместилась за время из положения, определяемого радиус-вектором в положение, определяемое радиус-вектором , то вектор называется Перемещением материальной точки, а длина части кривой между конечной и исходной точками – Путь .

Тогда средняя скорость перемещения - , а средняя скорость прохождения пути -

Закон сохранения количества движения (импульса) в векторной форме:

Положение центра масс системы определяется равенством:

Где - радиус-векторы отдельных малых тел системы в произвольной системе отсчета, - массы этих тел, - радиус-вектор центра масс системы.

Если материальная точка перемещается прямолинейно из положения в положение под действием постоянной силы , образующей угол с перемещением , то скалярное произведение вектора силы на вектор перемещения выражает работу этой силы по перемещению точки, т. е.

Кинетическая энергия тела массы , движущегося со скоростью , вычисляется по формуле:

Т. е. кинетическая энергия тела равна половине скалярного произведения импульса и скорости тела.

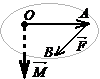
Если к точке приложена сила , и - некоторая точка пространства, то векторное произведение вектора на вектор силы выражает момент этой силы относительно точки , т. е. .

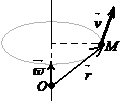
Линейная скорость точки твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется по формуле (где , - некоторая неподвижная точка оси вращения).

Силу, действующую на движущуюся частицу с зарядом в магнитном поле (сила Лоренца) можно вычислить по формуле:

Где - скорость частицы, - вектор магнитной индукции

< Предыдущая		Следующая >