12. Векторное произведение векторов

Упорядоченная тройка некомпланарных векторов называется Правой (левой), если после приведения к общему началу вектор располагается по ту сторону от плоскости, определяемой векторами и , откуда кратчайший поворот от к кажется совершающимся против часовой (по часовой) стрелки.

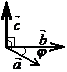
Для определения ориентации тройки векторов можно использовать также правило «правой руки» (правило «буравчика», правило «правого винта»).

Векторным произведением векторов и называется вектор , удовлетворяющий следующим требованиям:

1.

2.

3. Векторы образуют правую тройку векторов.

Алгебраические свойства:

1.

2.

3.

4.

Геометрические свойства:

1. Критерий коллинеарности векторов:

2. Длина векторного произведения равна площади параллелограмма, построенного на приведенных к общему началу векторах.

Выражение в декартовых координатах:

Если и , то

.

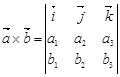< Предыдущая		Следующая >