10. Линейная независимость векторов, разложение вектора по базису

Выражение вида называется Линейной комбинацией векторов , где .

Векторы называются Линейно зависимыми, если существуют действительные числа , не все равные нулю, такие, что . Если это соотношение имеет место только при , то векторы называются Линейно-независимыми.

На плоскости любая пара неколлинеарных векторов является линейно независимой. В пространстве линейно независимыми являются любые три некомпланарных вектора. В частности, ортогональные векторы всегда линейно независимы.

Любая пара неколлинеарных векторов, лежащих в некоторой плоскости, образует базис этой плоскости. Аналогично, любая тройка некомпланарных векторов образует базис пространства.

Базис декартовой прямоугольной системы координат в пространстве образуют векторы , такие, что

Любой вектор пространства может быть единственным образом представлен в виде линейной комбинации базисных векторов этого пространства: , где - проекции вектора на координатные оси. При этом говорят, что Вектор разложен по базису, а коэффициенты разложения называют Координатами этого вектора в данном базисе.

Длина вектора . (1.1)

Пусть вектор Образует с координатными осями углы соответственно. Величины называются Направляющими косинусами вектора .

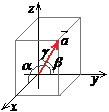
Координаты вектора могут быть вычислены по формулам:

(1.2)

Тогда:

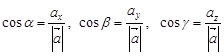(1.3)

При этом

В частности, координатами единичного вектора являются его направляющие косинусы, т. е.

Выражение линейных операций в декартовых координатах:

Пусть , , . Тогда:

Радиус-вектором точки называют вектор , начало которого находится в начале координат, конец – в точке . Координаты радиус-вектора совпадают с координатами точки.

Разложение радиус-вектора в базисе имеет вид:

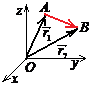
Отметим, что произвольный вектор может быть представлен в виде разности радиус-векторов точек и т. е.

, где .

< Предыдущая		Следующая >