Вариант № 01

Задача 1

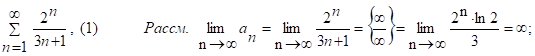
След. ряд (1) расх-ся, т. к. не вып-ся необходимый признак сход-ти числ. ряда.

Задача 2

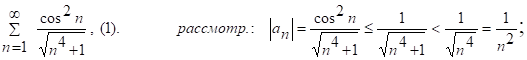
Но ряд 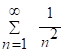- сходящийся гармонич. ряд, след. ряд (1) сх-ся по 1-Му признаку сравнения.

Задача 3

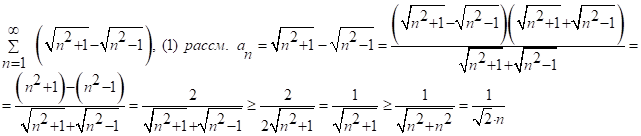
Но ряд - расх-ся гармонич. ряд, след. ряд (1) расх-ся по призн. сравнения.

Задача 4

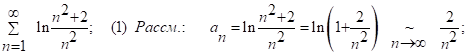
Но ряд 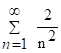- сх-ся гармон. ряд, след ряд (1) сх-ся по признаку сравнения.

Задача 5

след. ряд (1) расх-ся по признаку Даламбера.

Задача 6

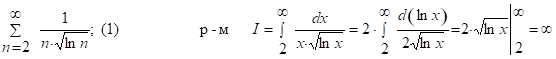След., несобственный инт-л I расх-ся, и вместе с ним расх-ся ряд (1) по интегральному признаку Коши.

Задача 7

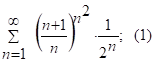
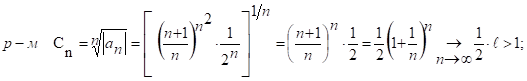
След ряд (1) расх-ся по радикальному признаку Коши.

Задача 8

- знакочередующийся ряд Лейбница;

А) р-м: но ряд 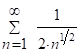- расх-ся гармонич. ряд,

След. ряд 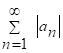- расх-ся по призн. сравнения, и след. ряд (1) не может сходиться абсолютно.

Б) Монотонно убывающая варианта при т. к. для :

, след. знакочередующийся ряд (1) сх-ся условно по т. Лейбница.

Ответ: ряд (1) сх-ся условно.

Задача 9

- знакочередующийся ряд Лейбница.

Р-м: 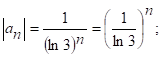но ряд 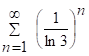представляет собой сход-ся геометрическую прогрессию , след ряд 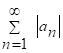- сх-ся и ряд (1) сх-ся абсолютно.

Задача 10

(1) – знакопеременный ряд;

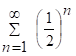Р-м: но ряд представ. собой

Сход-ся геометр. прогрессию , след ряд 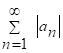сх-ся и ряд (1) сх-ся абсолютно.

Задача 11

(1) – степенной ряд

1) Р-м: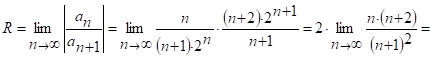

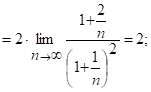След., степенной ряд (1) сх-ся абсолютно при , или .

2) Р-м поведение степенного ряда (1) на границе промежутка сх-ти, т. е. в т.

Р-м:

Р-м: - след. степенной ряд (1) расх-ся при (не выполн. необход. признак сх-ти числового ряда).

Ответ: Степ. ряд (1) сх-ся абсолютно при

Задача 12 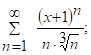(1) – степенной ряд.

1) р-м: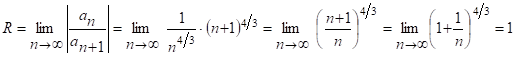

След., степ. ряд (1) сх-ся абсолютно при , т. е. при .

2) Р-м: поведение степ. ряда (1) на границе промежутка сх-ти, т. е. в т. ;

Р-м: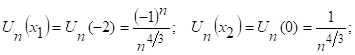

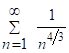ð но ряд - сх-ся гармонич. ряд,

След. степенной ряд (1) сх-ся абсолютно в т.

Ответ: Степенной ряд (1) сх-ся абсолютно при .

Задача 13

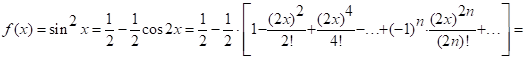
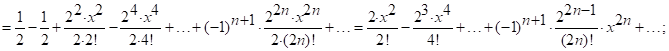
Полученный ряд сходится при .

Задача 14

;

Задача 15

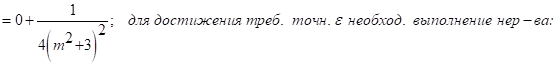
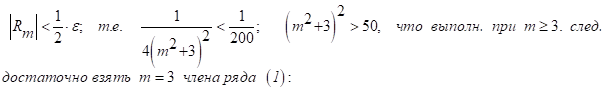
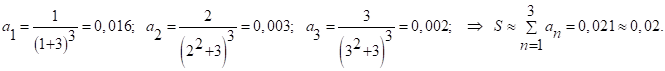
Задача 16

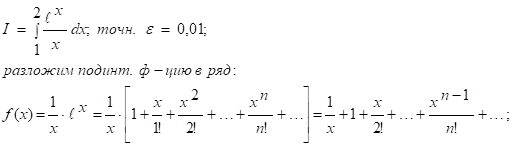
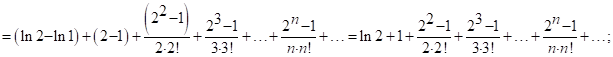
Полученный ряд - ряд с положительными членами; оценим его остаток:

Р-м: воспользуемся нер-вом: При ,

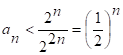=> - сх-ся геометрическая прогрессия.

=>

Для достижения требуемой точн. E должно выполняться: , что выполняется при что выполняется при , след. достаточно взять M=8 первых членов полученного ряда, не считая члена , т. е. всего нужно взять 9 членов ряда:

След.

Задача 17

Ищем решение Y(X) задачи Коши (1)-(2) в виде суммы степенного ряда (ряда Тейлора по степеням ):

Определим неизвестные коэффициенты этого разложения:

Продифференцируем равенство (1) по х:

Продифф. равенство (3) по х:

=> Искомое решение задачи (1)-(2) имеет вид:

Следующая >