58. Теорема Бернулли

Рассмотрим систему независимых испытаний Бернулли.

Система испытаний неограниченна. С каждым i-видом испытаний свяжем дискретную величину Xi

Хi принимают значения 1, если в i-том испытании произошло событие А и 0 - в противном случае

Рассмотрим случайную величину - число появлений события А в n испытаниях

Рассмотрим случайную величину

Это частость наступления события А в n испытаниях

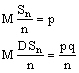
Используем неравенство Чебышева

Где e - произвольное неотрицательное число

Рассмотрим

Получена Теорема Бернулли.

Частость наступления произвольного события при числе испытаний стремящемся к бесконечности по вероятности сходится к теоретической вероятности наступления события.

Обоснование того, что - частость наступления события A заключается в следующем: с тоски зрения ранее приведенного определения, независимым испытаниям эквивалентны две схемы:

· проведение n раз одного и того же испытания

· проведение n независимых испытаний над n копиями одного и того же.

Аналогия: 100 раз монету подбрасывает 1 человек или 100 человек подбрасывают по одной монете.

< Предыдущая		Следующая >