57. Существующие определения сходимости случайных величин

Пусть имеется счетная последовательность случайных величин и пусть Предел последовательности.

1. Счетная последовательность сходится к пределу с вероятностью 1, если Р(А)=1.

Это не вероятность достоверного события.

2. Сходимость по поверхности.

Счетная последовательность случайных величин Сходится к По поверхности, если

3. Сходимость в среднеквадратичном.

Последовательность случайных величин сходится к пределу в среднеквадратичном, если выполняется

Покажем, что из сходимости в среднеквадратичном следует сходимость по вероятности.

Воспользуемся Неравенством Чебышева

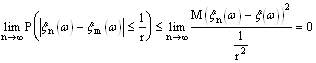
При любом конечном r если выполняется сходимость в среднеквадратичном, то этот предел существует и равен 0, т. к. числитель сходится к 0, а знаменатель конечен.

Теорема.

Счетная последовательность Сходится к пределу с вероятностью 1 только тогда, когда

Указанное выше событие Имеет своим дополнением событие

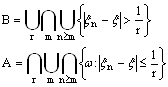
И сходимость с вероятностью 1 означает, что P(B)=0.

Очевидно, что условие теоремы достаточно рассмотреть для .

Положим

События Вrm, m=1,2,.... убывают, и для

Докажем это.

Будем искать P(Br) так

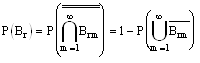
Событие, обратное имеет следующую структуру:

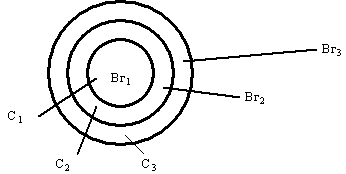
Показать самим, что следующее событие включает предыдущее.

По построению справедлива следующая формула

По третьей аксиоме теории вероятности

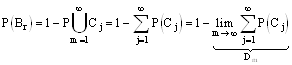
Построенный ряд D1, D2...Dn образует неубывающую ограниченную последовательность, следовательно имеет предел сверху.

Поэтому возможен переход

< Предыдущая		Следующая >