28. Аксиоматика. Формальная вероятностная модель

Имеется вероятностное пространство: (W, s, P). Зададим m числовых измеримых скалярных функций x1(w), ..., xm(w). Каждая из этих функций является одномерной по определению. Возьмем m произвольных действительных чисел и рассмотрим событие A.

Очевидно, что событие A является пересечением событий Ai вида:

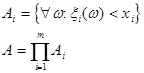
Т. к. каждое AiÎs-алгебре, то и AÌs-алгебре. Следовательно, существует вероятность наступления события A и существует числовая скалярная функция m действительных аргументов, которая определена для всех значений своих аргументов и численно равна вероятности наступления события A.

F(x1, x2, ...,xm)=P(A)

Это m-мерная функция распределения m-мерной случайной величены.

Свойства многомерного распределения:

1. Значение функции при значении хотя бы одного ее аргумента равного -¥, равно 0, как вероятность невозможного события.

2. Значение функции, при всех значениях ее аргументов равных +¥, равно 1, как вероятность достоверного события.

3. Функция не убывает по любой совокупности ее аргументов.

4. Функция непрерывна почти всюду (для инженерной практики это означает, что на конечном, либо счетном множестве аргументов она может иметь скачки 1-го рода).

Рассмотрим арифметическое пространство и зададим полуинтервалы вида:

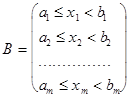
Доказать самим, что P(B) существует, и образ этого множества принадлежит s-алгебре по w.

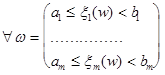
Можно доказать, что:

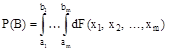
Т. о. многомерная функция распределения позволяет в m-мерном арифметическом пространстве задать счетно-аддитивную меру - функцию на поле, порожденному всеми m-мерными полуинтервалами объема ("i, ai¹bi). Тогда построим минимальную s-алгебру на этом поле, которая называется борелевским полем (алгеброй) в m-мерном арифметическом пространстве. Любая скалярная функция m-аргументов удовлетворяет всем свойствам, приведенным для m-мерной функции распределения и однозначно задает вероятностное пространство вида:

Таким образом, для инженерного исследования задача свелась к следующему: пространство элементарных событий - это m-мерное арифметическое пространство. По результатам статистических испытаний нужно оценить m-мерную функцию распределения F(x1, x2, ...,xm). Рассмотрим числовую скалярную функцию m действительных аргументов. g(x1, x2, ...,xm). Функция g(x1, x2, ...,xm) называется Борелевской, если для любого BÌb в одномерном арифметическом пространстве соответствующая . Тогда справедлива теорема, доказательство которой полностью повторяет доказательство в одномерном случае. Скалярная функция - является измеримой скалярной функцией - Случайной величиной.

< Предыдущая		Следующая >