7.3. Задачи для самостоятельного решения
7.1. Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу 4 приборов. Найти математическое ожидание и дисперсию этой случайной величины. Составить функцию распределения случайной величины и построить ее график.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
![]() ;
; ![]() .
.
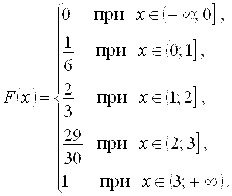
7.2. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины — числа импортных из 4 наудачу взятых телевизоров. Найти функцию распределения и построить ее график.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
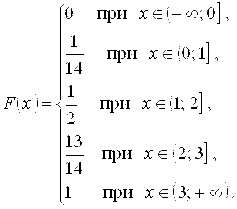
7.3. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй — 0,8, третьей — 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,006 |
0,092 |
0,398 |
0,504 |
![]() ;
;
![]() .
.
7.4. Поступающий в институт должен сдать 3 экзамена. Вероятность сдачи первого экзамена 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа приходов на экзамен для лица, поступающего в институт. Найти математическое ожидание случайной величины.
Ответ:
|
X |
1 |
2 |
3 |
|
P |
0,1 |
0,18 |
0,72 |
![]() .
.
7.5. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 10 %. Составить закон распределения числа банков, которые могут обанкротиться в течение следующего года и найти числовые характеристики этого распределения.
Ответ:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
![]() ;
;
![]() ;
;
![]() .
.
7.6. Вероятность поражения земляники вирусным заболеванием равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
![]() ;
;
![]() .
.
7.7. В урне находятся шары трех весов 3, 4 и 5 кг с соответствующими вероятностями 0,2; 0,3; 0,5. Извлекаются два шара с возвращением обратно. Составить закон распределения суммарного веса двух извлеченных шаров. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
6 |
7 |
8 |
9 |
10 |
|
P |
0,04 |
0,12 |
0,29 |
0,30 |
0,25 |
![]() ;
;
![]() .
.
7.8. Производится стрельба из орудия по удаляющейся цели. При первом выстреле вероятность попадания равна 0,8, при каждом следующем выстреле вероятность попадания уменьшается в 2 раза. Случайная величина Х — число попаданий в цель при трех выстрелах. Составить закон распределения случайной величины Х.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,096 |
0,472 |
0,368 |
0,064 |
7.9. Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5; 0,6; 0,7. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,06 |
0,29 |
0,44 |
0,21 |
![]() ;
;
![]() .
.
7.10. В лотерее разыгрывается один автомобиль стоимостью 5000 ден. ед., четыре телевизора – стоимостью 250 ден. ед. каждый, пять магнитофонов – стоимостью 200 ден. ед. каждый. Продано 1000 билетов стоимостью 7 ден. ед. каждый. Составить закон распределения случайной величины Х – чистого выигрыша, полученного участником лотереи, купившим один билет.
Ответ:
|
X |
– 7 |
193 |
243 |
4993 |
|
P |
0,990 |
0,005 |
0,004 |
0,001 |
7.11. В карточной игре игрок, который извлекает из колоды карт (52 карты) валет или даму, выигрывает 15 очков; тот, кто вытащит короля или козырного туза, выигрывает 5 очков. Игрок, который достанет любую другую карту, проигрывает 4 очка. Если вы решили участвовать в этой игре, определите сумму очков ожидаемого выигрыша.
Ответ:
|
Число очков |
15 |
5 |
– 4 |
|
|
|
|
|
![]() .
.
7.12. Дискретная случайная величина Х может принимать только два значения ![]() и
и ![]() , причем
, причем ![]() . Известны вероятность
. Известны вероятность ![]() возможного значения
возможного значения ![]() , математическое ожидание
, математическое ожидание ![]() И дисперсия
И дисперсия ![]() . Найти закон распределения этой случайной величины.
. Найти закон распределения этой случайной величины.
Ответ:
|
X |
3 |
4 |
|
P |
0,1 |
0,9 |
7.13. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго – 0,5. Пусть Х – число попаданий в мишень первым стрелком, Y– число попаданий в мишень вторым стрелком. Построить закон распределения случайной величины Z = X – Y и найти M(Z), D(Z).
Ответ: M(Z) = –0,2; D(Z) = 0,98.
7.14. Имеется шесть ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании замка, если испробованный ключ в последующих опробованиях не участвует. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ: M(Х) =![]() ; D(Х) =
; D(Х) = ![]()
7.15. В магазин поступила обувь с двух фабрик в соотношении 2 : 3. Куплено четыре пары обуви. Построить закон распределения числа купленных пар обуви, изготовленных первой фабрикой. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Ответ: M(Х) = 1,6; D(Х) = 0,96; ![]() .
.
7.16. В партии из десяти изделий имеется одно бракованное. Чтобы его обнаружить вынимают наугад одно изделие за другим и каждое вынутое изделие проверяют. Построить закон распределения и найти математическое ожидание числа проверенных изделий.
Ответ: M(Х) = 5,5.
7.17. Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти M(Х) и D(Х) случайной величины, если известно, что вероятность брака для каждой детали равна 0,1.
Ответ: M(Х) = 10;D(X)= 90.
7.18. Независимые случайные величины Х и Y заданы следующими законами распределения:
|
X |
5 |
2 |
4 |
Y |
7 |
9 | |
|
P |
0,6 |
0,1 |
0,3 |
Р |
0,8 |
0,2 |
Найти ![]() ,
, ![]() и проверить, что
и проверить, что ![]() =
=![]() ,
, ![]() .
.
Ответ: ![]() =11,8;
=11,8; ![]() = 32,56.
= 32,56.
7.19. Дискретная случайная величина задана законом распределения
|
|
0 |
1 |
2 |
3 |
|
|
|
0,2 |
|
0,5 |
Найти вероятность ![]() если известно, что
если известно, что ![]() в 2 раза больше, чем вероятность
в 2 раза больше, чем вероятность ![]()
Ответ: ![]() .
.
7.20. Найти дисперсию случайной величины ![]() если известно, что
если известно, что ![]()
Ответ: ![]() .
.
7.21. Найти дисперсию случайной величины ![]() если известно, что
если известно, что ![]()
Ответ: ![]() .
.
7.22. Даны две независимые случайные величины Х и Y; дисперсии которых равны ![]() Найти дисперсию
Найти дисперсию ![]()
Ответ: ![]() .
.
7.23. Даны две независимые случайные величины Х и Y; дисперсии которых равны ![]() Найти дисперсию
Найти дисперсию ![]()
Ответ: ![]() .
.
7.24. Даны законы распределения двух независимых случайных величин Х и Y.
|
|
1 |
2 |
|
0 |
2 |
3 | |||
|
|
0,6 |
0,4 |
|
0,1 |
0,2 |
0,7 |
Найти вероятность того, что случайная величина ![]() Примет значение, равное 4.
Примет значение, равное 4.
Ответ: ![]() .
.
7.25. Даны все возможные значения дискретной случайной величины Х: ![]() и
и ![]() Найти
Найти ![]()
Ответ: ![]() .
.
7.26. Даны все возможные значения дискретной случайной величины Х: ![]() и
и ![]() Найти
Найти ![]()
Ответ: ![]() .
.
7.27. Случайную величину умножили на постоянный множитель K. Как от этого изменится среднее квадратическое отклонение?
Ответ: Увеличится в ![]() раз.
раз.
| < Предыдущая | Следующая > |
|---|