3.1. Задачи для самостоятельного решения

3.1. Значения А и B равновозможны в квадрате , . Найти вероятности следующих событий: А = «корни квадратного трехчлена действительны», В = «корни квадратного трехчлена положительны».

Ответ:

3.2. Из отрезка наудачу взяты два числа. Какова вероятность того, что их сумма больше единицы, а произведение меньше единицы?

Ответ: .

3.3. На перекрестке установлен автоматический светофор, в котором одну минуту горит зеленый свет и полминуты красный, затем снова одну минуту — зеленый и полминуты красный и т. д. В случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность того, что он проедет перекресток без остановки?

Ответ:

3.4. К автобусной остановке через каждые четыре минуты подходит автобус линии А и через каждые шесть минут — автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего автобуса линии В равновозможен в пределах от нуля до четырех минут. Определить вероятность того, что: а) первый пришедший автобус окажется автобусом линии А; б) автобус какой-либо линии подойдет в течение двух минут.

Ответ: .

3.5. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стоянки первого парохода один час, а второго — два часа.

Ответ: Р = 0,121.

3.6. Иван и Петр договорились о встрече в определенном месте между одиннадцатью и двенадцатью часами. Каждый приходит в случайный момент указанного промежутка и ждет появления другого до истечения часа, но не более 15 мин, после чего уходит. Наблюдаемый результат — пара чисел (Х, у), где Х — время прихода Петра, У — время прихода Ивана. Определить вероятности следующих событий: А = «встреча состоялась», В = «Петр ждал Ивана все обусловленное время и не дождался», С = «Ивану не пришлось ждать Петра», D =
= «встреча состоялась после 11 ч 30 мин», Е = «Иван опоздал на встречу», F =
= «встреча состоялась, когда до истечения часа оставалось меньше пяти минут».

Ответ:

3.7. Какова вероятность не целясь попасть бесконечномалой пулей в квадратную решетку, если толщина прутьев равна А, а расстояние между их средними линиями равно L?

Ответ: .

3.8. На окружности единичного радиуса наудачу ставятся три точки А, В и С. Какова вероятность того, что треугольник АВС остроугольный?

Ответ:

3.9. В круге радиуса проводятся хорды параллельно заданному направлению. Какова вероятность того, что длина наугад взятой хорды не более , если равновозможны любые положения точек пересечения хорды с диаметром, перпендикулярным выбранному направлению?

Ответ:

3.10. В шар вписан правильный тетраэдр. Найти вероятность того, что случайно брошенная в шар точка окажется внутри тетраэдра.

Ответ: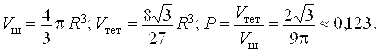

< Предыдущая		Следующая >