Тема 1. Элементы комбинаторики. Теоретические сведения

При выборе M элементов из N различных элементов говорят, что они образуют Соединение из N элементов по M. Различают три вида соединений элементов:

1. Размещениями называются соединения, которые отличаются друг от друга составом элементов или их порядком, и каждое из которых содержит M элементов, взятых из N различных элементов.

Например, выпишем все размещения элементов a, b, c, d по два: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

2. Перестановками из N элементов называются соединения, каждое из которых содержит N различных элементов, взятых в определенном порядке.

Например, выпишем все перестановки из элементов a, b, c: abc, acb, bac, bca, cab, cba.

3. Сочетаниями из N элементов по M называются соединения, отличающиеся друг от друга, по крайней мере, одним элементом, каждое из которых содержит M элементов, взятых из N различных элементов.

Например, выпишем все сочетания из элементов a, b, c, d, e по три: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Задача о числе размещений: Сколькими способами можно выбрать и разместить по M различным местам N разных предметов? Количество таких способов обозначается и читается: «Число размещений из N по M».

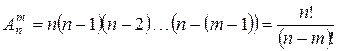, (по определению)

Пример 1. Сколько всего пятизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?

Решение. Это задача о выборе и размещении по пяти разным местам пяти из десяти различных цифр. Поэтому число указанных телефонных номеров равно .

Пример 2. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

Решение. Поскольку нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр. Следовательно, указанных чисел имеется .

Задача о числе перестановок: Сколькими способами можно переставить N разных предметов, расположенных на N разных местах? Количество таких способов обозначается и читается: «Число перестановок из N».

, (по определению)

Пример 1. Сколько всего шестизначных четных чисел можно составить из цифр 1, 3, 4, 5, 7, 9, если в каждом из этих чисел ни одна цифра не повторяется?

Решение. Из всех указанных цифр последней может быть только цифра 4. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Значит, нужно найти число перестановок из пяти элементов. . Таким образом, можно составить 120 указанных чисел.

Пример 2. Сколькими способами семь книг разных авторов можно поставить на полке в один ряд?

Решение. Эта задача о числе перестановок семи разных книг . Следовательно, имеется 5040 способов осуществить расстановку книг.

Задача о числе сочетаний: Сколькими способами можно выбрать M из N разных предметов? Количество таких способов обозначается и читается: «Число сочетаний из N по M».

; ;.

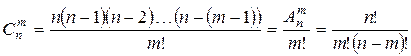Пример 1. Сколькими способами читатель может выбрать две книжки из пяти имеющихся?

Решение. Искомое число способов равно числу сочетаний из пяти по два. Так как , то указанную выборку читатель может осуществить десятью способами.

Пример 2. В выпуклом семиугольнике проведены всевозможные диагонали, при этом никакие три из них не пересекаются в одной точке. Сколько точек пересечения указанных диагоналей?

Решение. Каждой точке пересечения диагоналей соответствуют четыре вершины семиугольника, а каждой четверке вершин семиугольника соответствует одна точка пересечения. Поэтому число всех точек пересечения диагоналей равно числу способов, которыми среди семи вершин можно выбрать четыре вершины. Поскольку , то число точек пересечения диагоналей равно 35.

Правило сложения

Если некоторый предмет может быть выбран из совокупности предметов способами, а другой предмет может быть выбран способами, то выбрать либо , либо можно способами. Правило распространяется на совокупность .

Правило умножения

Если некоторый предмет можно выбран из совокупности предметов способами и после каждого такого выбора предмет может быть выбран способами, то пара объектов (,) в указанном порядке может быть выбрана способами. Правило распространяется на совокупность .

Пример 1. Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?

Решение. В указанной комиссии может быть либо один математик и семь экономистов, либо два математика и шесть экономистов. Выбор одного математика из двух возможен способами, а семи экономистов из десяти – способами. По правилу произведения число способов выбора комиссии из одного математика и семи экономистов равно . Выбор двух математиков из двух возможен способом, а шести экономистов из десяти – способами. По правилу произведения число способов выбора комиссии из двух математиков и семи экономистов равно . Общее число способов выбора комиссии с одним или с двумя математиками по правилу сложения равно .

Пример 2. Сколько существует делителей числа 210?

Решение. Разложим данное число на простые множители: . Число делителей, составленных из произведения двух простых множителей, равно (это числа 6, 10, 14, 15, 21, 35); число делителей, составленных из произведения трех простых множителей, равно (это числа 30, 42, 70, 105); число простых делителей равно четырем (это числа 2, 3, 5, 7). Кроме того, делителями являются число 1 и число 210. Итак, согласно правилу сложения, число всех делителей равно .

До сих пор рассматривались соединения, в каждое из которых любой из N различных элементов входит один раз. Можно рассматривать соединения с повторениями.

Размещения с повторениями. Например, выпишем размещения по три из элементов 4 и 5 с повторениями: 444, 445, 454, 544, 555, 554, 545, 455.

Задача о числе размещений с повторениями: Сколькими способами можно разместить по M различным местам любые M предметов, выбранных из N различных предметов с повторениями каждого из них любое число раз, но не более M?

.

Пример 1. Каждый телефонный номер состоит из 5 цифр. Сколько всего телефонных номеров, содержащих только цифры 2, 3, 5 и 7?

Решение. Это задача о числе размещений в пяти разных местах пяти цифр, выбранных из четырех разных цифр с повторениями каждой из них любое число раз, но не более пяти. Так как , то число всех указанных телефонных номеров равно 1024.

Пример 2. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно . Число всех букв, каждая из которых записывается двумя символами, равно . Число всех букв, каждая из которых записывается тремя символами, равно . Число всех букв, каждая из которых записывается четырьмя символами, равно . Число всех букв, каждая из которых записывается пятью символами, равно . Число всех указанных букв равно 62.

Перестановки с повторениями – перестановки из N предметов, в каждую из которых входят одинаковых предметов одного типа, одинаковых предметов другого типа и т. д. . Например, выпишем перестановки с повторениями цифр 4 и 5, каждая из которых взята по два раза: 4455, 5544, 4545, 5454, 4554, 5445.

Задача о числе перестановок с повторениями: Сколькими способами можно переставить N предметов K различных типов каждого типа соответственно одинаковых предметов, расположенных на n разных местах?

.

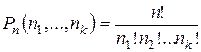Пример 1. Сколькими способами можно расположить в ряд 2 зеленые и 4 красные лампочки?

Решение. способами.

Пример 2. Сколькими способами можно переставить буквы в слове какао, чтобы получались всевозможные различные наборы букв?

Решение. способами.

Сочетания с повторениями. Например, выпишем все сочетания из трех цифр 3, 4,5 по два с повторениями: 33, 34 (43), 35 (53), 44, 45 (54), 55.

Задача о числе сочетаний с повторениями: Если имеется по M одинаковых предметов каждого из N различных типов, то сколькими способами можно выбрать M из этих M×N предметов?

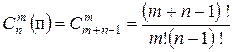
Пример 1. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырех пирожных?

Решение. способов.

Пример 2. Сколькими способами можно выбрать четыре монеты из четырех пятирублевых и из четырех двухрублевых монет?

Решение. способов.

Следующая >