20. Биномиальный закон распределения
Пусть заданы числа N принадлежит N 1). Тогда каждому целому числу из промежутка [0; N] можно поставить в соответствие вероятность, рассчитанную по формуле Бернулли. Получим закон распределения случайной величины (назовём её b)
|
B |
0 |
¼ |
K |
¼ |
N |
|
Р |
¼ |
¼ |
|
¼ |
¼ |
Будем говорить, что случайная величина b распределена по закону Бернулли. Такой случайной величиной является частота появления события А в N повторных независимых испытаниях, если в каждом испытании событие А происходит с вероятностью P.
Рассмотрим отдельное I-Е испытание. Пространство элементарных исходов для него имеет вид
![]()
Определим на этом пространстве случайную величину xI следующим образом:
xI = 1, если происходит событие А;
xI = 0, если происходит событие ![]()
Закон распределения случайной величины xI рассматривался в предыдущем параграфе.
|
XI |
1 |
0 |
|
Р |
P |
Q = 1–P |
MX = ×Р; DX = Рq
Для I = 1,2,¼,N получаем систему из N независимых случайных величин xI, имеющих одинаковые законы распределения. Если теперь сравнить законы распределения двух случайных величин b и ![]() , то можно сделать очевидный вывод: b =
, то можно сделать очевидный вывод: b = ![]() . Отсюда следует, что для случайной величины b, имеющей закон распределения Бернулли, математическое ожидание и дисперсия определяются формулами
. Отсюда следует, что для случайной величины b, имеющей закон распределения Бернулли, математическое ожидание и дисперсия определяются формулами
MB = M![]() =
= 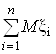 =
= ![]() = Np;
= Np;
DB = D![]() =
= 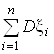 =
= ![]() = Npq
= Npq
Найдём оценку величины Р — вероятности успеха в одном испытании некоторого биномиального эксперимента. Для этого проведём N Испытаний и подсчитаем Х – число успехов. Оценку Р* неизвестной величины Р определим формулой Р* = ![]() .
.
Пример.
Из 20 отобранных для контроля образцов продукции 4 оказались нестандартными. Оценим вероятность того, что случайно выбранный экземпляр продукции не отвечает стандарту отношением Р* = 4/20 = 0,2.
Так как Х случайная величина, Р* – тоже случайная величина. Значения Р* могут меняться от одного эксперимента к другому (в рассматриваемом случае экспериментом является случайный отбор и контроль 20-ти экземпляров продукции). Каково математическое ожидание Р*? Поскольку Х есть случайная величина, обозначающая число успехов в N испытаниях по схеме Бернулли, МX = Np. Для математического ожидания случайной величины Р* по определению получаем: Mp* = M![]() , но N Здесь является константой, поэтому по свойству математического ожидания
, но N Здесь является константой, поэтому по свойству математического ожидания
Mp* = ![]()
Таким образом, “в среднем” получается истинное значение Р, чего и следовало ожидать. Это свойство оценки Р* величины Р имеет название: Р* является Несмещённой Оценкой для Р. Отсутствие систематического отклонения от величины оцениваемого параметра Р подтверждает целесообразность использования величины Р* в качестве оценки. Вопрос о точности оценки пока оставляем открытым.
| < Предыдущая | Следующая > |
|---|