24. Решение позиционной игры с полной информацией
Решение позиционной игры с полной информацией легко решается в соответствии с теоремой Куна, утверждающей, что данная игра разрешима по доминированию, т. е. для каждого из игроков имеются доминирующие стратегии, которые и необходимо применять.
Для того, чтобы это продемонстрировать, рассмотрим описанную выше игру «Выборы с правом вето». Поскольку из всех вершин, предшествующих конечным, ходит игрок 3, то остальные игроки, зная его функцию выигрыша U3, могут легко предвидеть его решения. Это позволяет привести игру, изображенную на рис.3.1 к следующей:
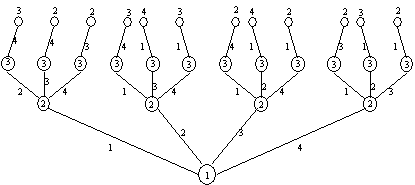
Рис.3.3
Поскольку в новом дереве игрок 3 уже по существу не принимает решения, то финальная вершина определяется ходами игрока 2. Игрок 1, зная функцию выигрышей U2, может предвидеть поведение игрока 2. В итоге получается игра с одним участником – первым игроком и следующим деревом игры:

Рис.3.4
Поскольку для первого игрока желательна победа четвертого претендента, то он отклонит третьего претендента. Далее второй игрок вынужден будет отклонить второго претендента, а третий игрок – первого. Выигрыши игроков в данной игре равны 7, 4 и 4 соответственно.
Таким образом алгоритм решения позиционных игр с полной информацией, в соответствии с теоремой Куна, состоит в том, что начиная с последнего хода последовательно отбрасываются заведомо худшие для игрока, делающего этот ход, решения. После всех таких редукций получаем решение в чистых стратегиях.
| < Предыдущая | Следующая > |
|---|