11. Решение матричной игры (2х2)
Пусть матричная игра G (2x2) имеет платежную матрицу
|
Ai |
B1 |
B2 |
|
A1 |
A11 |
A12 |
|
A2 |
A21 |
A22 |
Предположим, что игра не имеет седловой точки, т. е. a¹b. При наличии седловой точки решение очевидно.
В соответствии с основной теоремой игра имеет оптимальное решение в смешанных стратегиях: SA=||p1, p2|| и SB=||q1, q2||, где вероятности применения (относительные частоты применения) чистых стратегий удовлетворяют соотношениям
![]() ; (2.11)
; (2.11)
![]() . (2.12)
. (2.12)
В соответствии с теоремой об активных стратегиях, оптимальная смешанная стратегия обладает тем свойством, что обеспечивает игроку максимальный средний выигрыш, равный цене игры N, независимо от того, какие действия предпринимает другой игрок, если тот не выходит за пределы своих активных стратегий. В частности, если игрок А использует свою оптимальную смешанную стратегию, а игрок В - свою чистую активную стратегию В1, то цена игры N равна
![]() , (2.13)
, (2.13)
А при использовании игроком В чистой активной стратегии В2, выигрыш будет равен
![]() . (2.14)
. (2.14)
Уравнения (2.11), (2.13) и (2.14) образуют систему трех линейных алгебраических уравнений с тремя неизвестным:
Р1, р2 и n.
Решая ее, легко находим, что
![]() . (2.15)
. (2.15)
![]() . (2.16)
. (2.16)
![]() . (2.17)
. (2.17)
Если игрок В использует свою оптимальную смешанную стартегию, а игрок А - свою чистую активную стратегию А1, то цена игры N равна
![]() , (2.18)
, (2.18)
А при использовании игроком А чистой активной стратегии А2, выигрыш будет равен
![]() . (2.19)
. (2.19)
Уравнения (2.12), (2.18) и (2.19) образует систему трех линейных алгебраических уравнений с тремя неизвестными: q1; q2 и n.
Решая ее, легко находим, что
![]() . (2.20)
. (2.20)
![]() . (2.21)
. (2.21)
![]() . (2.22)
. (2.22)
Естественно, что в обоих случаях цена игры (выражения (2.17) и (2.22)) получилась одна и та же.
Чтобы соотношения (2.15), (2.16), (2.17), (2.20), (2.21), (2.22) имели смысл, необходимо потребовать, чтобы

Или
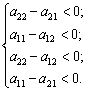
Тогда 0<p1<1; 0<p2<1; 0<q1<1; 0<q2<1.
Нетрудно заметить, что в этих неравенствах отражено предположение об отсутствии в рассматриваемой игре седловой точки. Действительно, ни один из четырех выигрышей а11, а12, а21, а22 не может удовлетворить этим неравенствам, будучи минимальным в своей строке и максимальным в своем столбце.
Решения системы уравнений (2.15), (2.16), (2.17) и (2.20), (2.21), (2.22), полученные алгебраическим методом, удобно получать и графическим методом (рис. 2.4). Для нахождения вероятностей Р1, Р2 и цены игры V в прямоугольной системе координат по оси абсцисс откладывается вероятность Р1Î[0,1], а по оси ординат - соответствующие этой вероятности - выигрыши игрока А.
При р1=0, игрок А применяет чистую стратегию А2. Если при этом игрок В применяет чистую стратегию В1, то выигрыш игрока А равен а21 (уравнение (2.13)), а если игрок В применяет чистую стратегию В2, то выигрыш игрока А равен а22 (уравнение (2.14)). При р1=1, игрок А применяет чистую стратегию А1.
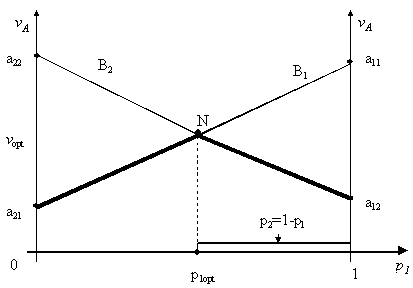
Рис. 2.4
Если при этом игрок В применяет чистую стратегию В1, то выигрыш игрока А равен а11, а при применении чистой стратегии В2 - а12. Так как значения р1 лежат в пределах [0,1], то соединяя крайние точки для стратегий В1 и В2 (строя графики функций VА=(a11-a21)p1+a22 и VА=(a12-a22)p1+a22), получаем значения выигрышей игрока А для всех промежуточных значений Р1.
В соответствии с принципом максимина, игрок А должен выбрать такую смешанную стратегию, при которой его минимальный выигрыш максимален. Точка N пересечения отрезков прямых (рис. 2.4) и определяет как оптимальную цену игры VOpt, так и оптимальные вероятности P1opt и P2opt=1-P1opt, соответствующие оптимальной смешанной стратегии игрока А, т. е. дает решения системы уравнений (2.11), (2.13), (2.14).
Для графического решения системы уравнений (2.12), (2.18), (2.19) отложим по оси абсцисс вероятность q1Î[0,1], а по оси ординат соответствующие этой вероятности выигрыши игрока В:
VВ=(a11-a12)q1+a12; (2.23)
VВ=(a21-a22)q1+a22. (2.24)
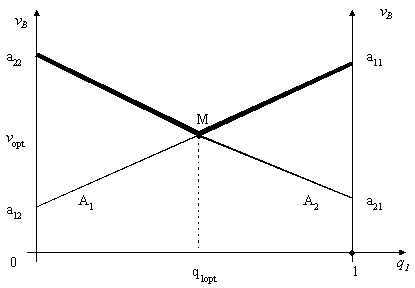
Рис. 2.5
Решением являются координат точки М пересечения прямых, описываемых уравнений (2.23) и (2.24):
Q1opt;q2opt=1-q1opt и VOpt.
Это же следует и из принципа максимина, в соответствии с которым игрок В должен выбрать такую смешанную стратегию, при которой его максимальный проигрыш будет минимальным.
Для игры G(2х2) с седловой точкой геометрическая интерпретация решения быть представлена, например, следующим образом (рис.2.6).

Рис. 2.6
Стратегия В2 игрока В является для него явно невыгодной, так как, применяя ее, он в любой случае проигрывает больше, чем при применении стратегии В1. В данной игре Р1Opt=1;р2Opt=0; VOpt=а11, т. е. игра имеет седловую точку N и решается в чистых стратегиях. Игрок А должен применять стратегию А1, а игрок В - стратегию В1.
На рис. 2.7 показан случай, в котором решением игры для игрока А является чистая стратегия А2, а для игрока В - стратегия В1.
Игра имеет седловую точку N.
Пример: Найти алгебраическим и геометрическим методами решение игры, платежная матрица которой имеет вид
|
Ai |
B1 |
B2 |
AI |
|
A1 |
4 |
-2 |
-2 |
|
A2 |
1 |
3 |
1 |
|
BJ |
4 |
3 |

Рис. 2.7
В данной игре нижняя цена игры a=1 не равна верхней цены игры b=3, поэтому игра не имеет седловой точки и, в соответствии с основной теоремой матричных игр, имеет оптимальное решение в смешанных стратегиях.
Для игрока А, в соответствии с формулами (2.15) и (2.16), оптимальные вероятности применения стратегий А1 и А2 равны:
![]() ;
;
![]() .
.
Для игрока В, в соответствии с формулами (2.20) и (2.21), оптимальные вероятности применения стратегий В1 и В2 равны:
![]() ;
;
![]() .
.
Таким образом, оптимальные смешанные стратегии игроков ![]() ;
; ![]() , а цена игры в соответствии с формулой (2.22) равна:
, а цена игры в соответствии с формулой (2.22) равна:
![]() .
.
Так как N>0, то игра выгодна для игрока А.
Графическое изображение игры для игрока А показана на рис. 2.8.

Рис. 2.8
Нижняя граница выигрыша игрока А определяется ломаной CND. Оптимальное решение, определяется точкой N, естественно, дает тоже решение, что и алгебраический метод: ![]() .
.
Геометрическое изображение игры для игрока В показано на рис.2.9.

Рис. 2.9
Оптимальное решение, определяемое точкой М, дает решение ![]() .
.
| < Предыдущая | Следующая > |
|---|
 Bj
Bj