1.3.1. Решение матричных игр в чистых стратегиях

Целью участников любой матричной игры является выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В минимальный проигрыш.

Определение. Чистую стратегию Ai игрока А называют оптимальной, если при ее применении выигрыш игрока А не уменьшается, какими бы своими стратегиями не пользовался игрок В. Оптимальной для игрока В называют чистую стратегию Bj, при использовании которой проигрыш игрока В не увеличивается, какие бы стратегии не применял игрок А.

При поиске оптимальных стратегий опираются на основополагающий принцип теории игр – принцип осторожности, в соответствии с которым каждый игрок, считая партнера по игре весьма разумным соперником, выбирает свои стратегии с учетом того, что противник ни в коем случае не упустит ни единой возможности использовать любую его ошибку в своих интересах. Поэтому игроки должны быть предельно внимательны при выборе каждый своей чистой стратегии.

Предположим, что игроку А надлежит сделать свой выбор. Анализируя платежную матрицу (aij)i=1,m j=1,n он для каждой чистой стратегии Ai сначала найдет минимальное значение ожидаемого выигрыша:

А затем из всех выделит наибольшее

И выберет соответствующую ему чистую стратегию Ai. Это и будет наиболее предпочтительная в данных условиях стратегия игрока А. Ее называют максиминной, поскольку она отвечает величине

(1)

Определение. Число , определяемое по этой формуле называется нижней чистой ценой игры (максимином). Оно показывает, какой минимальный выигрыш может получить игрок А, правильно применяя свои чистые стратегии при любых действиях игрока В.

Игрок В при оптимальном своём поведении должен стремиться по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока А. Поэтому для игрока В отыскивается число

Т. е. определяется максимальный выигрыш игрока А, при условии, что игрок В применит свою J-ю чистую стратегию, затем игрок В отыскивает такую свою стратегию, при которой игрок А получит минимальный выигрыш, т. е. находит число

(2)

Определение. Число , определяемое по формуле (2), называется чистой верхней ценой игры (минимаксом) и показывает, какой минимальный проигрыш за счёт своих стратегий может себе гарантировать игрок В (что соответственно определяет максимальный выигрыш игрока А при выборе правильных стратегий игроком В).

Другими словами, применяя свои чистые стратегии игрок А может обеспечить себе выигрыш не меньше , а игрок В за счёт применения своих чистых стратегий может не допустить выигрыш игрока А больше, чем .

Определение. Если в игре с матрицей А a=b, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры v ==

Седловая точка – определяет пару чистых стратегий (iо, jо) соответственно игроков А и В, при которых достигается равенство =. В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем так же придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе:

(3)

Где I, j – любые чистые стратегии соответственно игроков 1 и 2; (iо, jо) – стратегии, образующие седловую точку.

Таким образом, исходя из (3), седловой элемент является минимальным в iо-й строке и максимальным в jо-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: В матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (iо, jо) игроков 1 и 2, образующая седловую точку и седловой элемент , называется решением игры. При этом Iо и Jо называются оптимальными чистыми стратегиями соответственно игроков А и В.

Пример 1

Седловой точкой является пара (Iо = 3; Jо = 1), при которой цена игры v===2.

Заметим, что хотя выигрыш в ситуации (3;3) также равен 2, она не является седловой точкой, т. к. этот выигрыш не является максимальным среди выигрышей третьего столбца.

Пример 2 (см. Пример 1 из п. 1.2) Анализируя платежную матрицу игры, можно найти нижнюю чистую цену игры – минус 2. Таким образом, для игрока А максиминной стратегией будет являться А2 – запись чисел 1 и 2. Верхняя чистая цена игры равна двум, а минимаксной стратегией для игрока В является В2 – запись такой же числовой комбинации. Так что по разумным соображениям эта игра обречена на ничью.

Пример 3

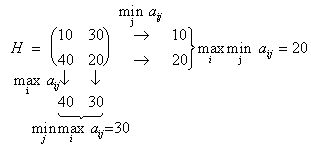
Из анализа платежной матрицы H видно, что <, т. е. данная матрица не имеет седловой точки. Если игрок А выбирает свою чистую максиминную стратегию I = 2, то игрок В, выбрав свою минимаксную J = 2, проиграет только 20. В этом случае игроку А выгодно выбрать стратегию i = 1, т. е. отклониться от своей чистой максиминной стратегии и выиграть 30. Тогда игроку В будет выгодно выбрать стратегию j = 1, т. е. отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь игрок А должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а игрок В ответит выбором 2-й стратегии и т. д.

Теорема 1. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т. е. .

Доказательство. По определению ; . Объединяя эти соотношения, получим . Отсюда или . Это неравенство справедливо при любых комбинациях i и j. Будет оно справедливо и для тех i и j, для которых реализуются максимальное и минимальное значения и . Что и требовалось доказать.

Исследование в матричных играх начинается с нахождения её седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что игрок А не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью. Об этом будет рассказано в следующем разделе.

< Предыдущая		Следующая >