2.3. Минимальный путь в нагруженном ориентированном графе

Найти минимальный путь в нагруженном ориентированном графе из вершины в вершину по методу Форда-Беллмана.

Рассмотрим сначала общую задачу – нахождения минимального пути из вершины VНач в VКон.

Пусть D=(V,X) – нагруженный ориентированный граф, V={V1,…,Vn}, N>1. Введем величины , где I=1,…,N, K=0,1,2,…,N–1.

Для каждого фиксированного I и K величина равна длине минимального пути среди путей из VНач в Vi содержащих не более K дуг. Если путей нет, то .

Положим также .

Составляем матрицу длин дуг C(D)=[Cij] порядка N:

Утверждение. При I=2,…,N, K³0 выполняется равенство

. (3.1)

Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе D из VНач в VКон.( VНач ≠ VКон)

записываем в виде матрицы, I- строка, K-столбец.

1) Составляем таблицу , I=1,…,N, K=0,…,N-1. Если , то пути из VНач в VКон нет. Конец алгоритма.

2) Если то это число выражает длину любого минимального пути из VНач в VКон. Найдем минимальное K1³1, при котором . По определению получим, что K1- минимальное число дуг в пути среди всех минимальных путей из VНач В VКон.

3) Затем определяем номера I2,…, такие, что

,

,

,

То есть, восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из VНач в VКон.

Пример

Найдем минимальный путь из вершины V2 в V6 в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин N=7, следовательно, матрица длин дуг ориентированного графа D Будет иметь размерность 7×7.

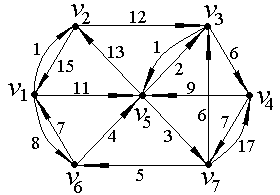
Рис. 9.

Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

.

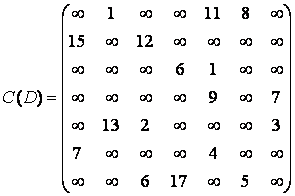Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины V2 в вершину Vi не более, чем за K шагов, K=0,…N-1 (N=7, следовательно, K=0,…6). Как было определено выше, , и для всех остальных вершин Vi ≠ V2, то есть первый столбец таблицы состоит из элементов, равных , кроме элемента . Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины V2 за один шаг. Далее по формуле (3.1) находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент , складываем элементы столбца и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел:

.

В конечном итоге получаем следующую таблицу:

Теперь необходимо по построенной таблице и по матрице C(D) восстановить минимальный путь из вершины V2 в V6, который будет строиться с конца, то есть, начиная с вершины V6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей V6 в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину V6 мы можем попасть за один шаг из вершин V1 и V7 (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C(D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину V7 можно попасть из V4 и V5 (длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины V2 в V6: V2 V3 V5 V7 V6.

< Предыдущая		Следующая >