2.2. Расстояния в ориентированном графе

С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры.

Пусть ориентированный граф с n³2 вершинами и V,W (V¹W) – заданные вершины из V.

Алгоритм поиска минимального пути из в в ориентированном графе

(Алгоритм фронта волны).

1) Помечаем вершину индексом 0, затем помечаем вершины Î образу вершины индексом 1. Обозначаем их FW1 (V). Полагаем K=1.

2) Если или K=N-1, и одновременно то вершина не достижима из . Работа алгоритма заканчивается.

В противном случае продолжаем:

3) Если , то переходим к шагу 4.

В противном случае мы нашли минимальный путь из в и его длина равна K. Последовательность вершин

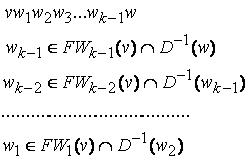
Есть этот минимальный путь. Работа завершается.

4) Помечаем индексом K+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом K. Множество вершин с индексом K+1 обозначаем . Присваиваем K:=K+1 и переходим к 2).

Замечания

· Множество называется фронтом волны KГо уровня.

· Вершины могут быть выделены неоднозначно, что соответствует случаю, если несколько минимальных путей из в .

Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу расстояний R(D) между его вершинами. Это квадратная матрица размерности , элементы главной диагонали которой равны нулю (, I=1,..,N).

Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний (, если ). Далее построчно заполняем матрицу следующим образом.

Рассматриваем первую строку, в которой есть единицы. Пусть это строка − I-тая и на пересечении с J-тым столбцом стоит единица (то есть ). Это значит, что из вершины можно попасть в вершину за один шаг. Рассматриваем J-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент . Тогда из вершины в вершину можно попасть за два шага. Таким образом, можно записать . Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.

Примечание. Самый длинный путь найти при помощи алгоритма фронта волны.

Пример

Найдем расстояния в ориентированном графе D, изображенном на рис. 7. В данной задаче количество вершин N=7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D Будут иметь размерность 7×7.

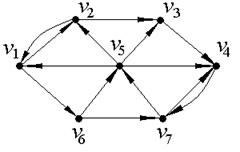
Рис.7.

Матрица смежности:

.

Начинаем заполнять матрицу R(D) минимальных расстояний: сначала ставим нули по главной диагонали и Rij=Aij, если Aij=1, (т. е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать . Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит, , . Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому . В итоге получаем следующую матрицу:

.

Таким образом, диаметром исследуемого ориентированного графа будет .

Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше : R(Vi) − максимальное из расстояний, стоящих в I-той строке. Таким образом,

R(V1)=3, R(V2)=3, R(V3)=5, r(V4)=4, r(V5)=2, r(V6)=2, r(V7)=3.

Значит, радиусом графа G будет

Соответственно, центрами графа G Будут вершины V5 и V6 , так как величины их эксцентриситетов совпадают с величиной радиуса.

Опишем теперь нахождение минимального пути из вершины V3 в вершину V6 по алгоритму фронта волны. Обозначим вершину V3 как V0, а вершину V6 - как W (см. рис. 8).

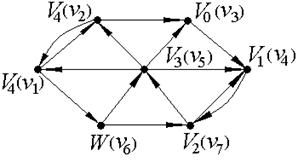
Рис.8.

Множество вершин, принадлежащих образу V0, состоит из одного элемента - это вершина V4, которую, согласно алгоритму, обозначаем как V1: FW1(V3)={V4}. Поскольку искомая вершина не принадлежит фронту волны первого уровня , продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V1: FW2(V3)={V7}, обозначаем V7≡V2. В образ вершины V2 входят две вершины - V5 и V4, но, так как V4 уже была помечена как V0, то фронт волны третьего уровня состоит из одного элемента: FW3(V3)={V5}, V5≡V3. Из непомеченных вершин в образ вершины V3 входят V1 и V2, соответственно, FW4(V3)={V1, V2}, V1≡V4, V2≡V4. Теперь помечены все вершины, кроме V6, которая входит в образ вершины , то есть FW5(V3)={V6≡W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины V3 в вершину V6: V3 V4 V7 V5 V1 V6.

< Предыдущая		Следующая >