1. Краткий перечень основных понятий теории графов
Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 1, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.
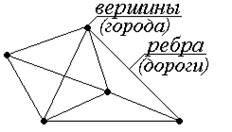
Рис. 1.
Формальное определение графа таково [1-8]. Графом Г=(V,X) называется пара множеств: V – множество, элементы которого называются Вершинами, X – множество неупорядоченных пар вершин, называемых Ребрами. Если V, W Î V, X=(V,W)ÎX, то говорят, что ребро X соединяет вершины V и W или X инцидентно V и W. Таким образом, {v, w} – обозначение ребра. Если Х представляет собой упорядоченные пары (т. Е. X – подмножество декартова произведения V×V), то граф называется ориентированным, а пары {v, w} называют дугами. Если множеству X принадлежат пары V=W, то такие ребра (V,V) называют петлями. Существование одинаковых пар {v, w} соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер называют количество таких одинаковых пар.
Например, кратность ребра {V1, v2} в графе, изображенном на рис. 2, равна двум, кратность ребра {V3, v4} − трем.
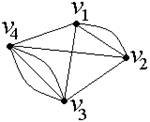
Рис.2.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель.
Заметим, что Графом также называют мультиграф, в котором ни одна пара не встречается более одного раза.
Итак, используемые далее Обозначения:
V – множество вершин;
X – множество ребер или дуг;
V (или Vi)– вершина или номер вершины;
G, G0 – неориентированный граф;
D, D0 – ориентированный;
{V,W} − ребра неориентированного графа;
{V,V} – обозначение петли;
(V,W) − дуги в ориентированном графе;
V,W – вершины, X,Y,Z – дуги и ребра;
N(G), N(D) количество вершин графа;
M(G) – количество ребер, M(D) – количество дуг.
Примеры
1) Ориентированный граф D=(V, X), V={V1, V2, V3, V4},
X={X1=(V1,V2), x2=(V1,V2), X3=(V2,V2), X4=(V2,V3)}.
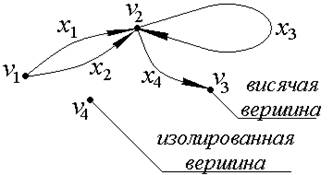
Рис. 3.
2) Неориентированный граф, изображенный на рис. 4:
G=(V, X), V={V1, V2, V3, V4, V5},
X={X1={V1,V2}, X2={V2,V3}, X3={V2,V4}, X4={V3,V4}}.
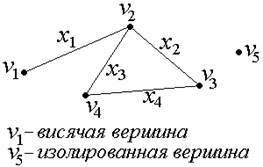
Рис. 4.
| < Предыдущая | Следующая > |
|---|