75. Выражение решения задачи Дирихле через функцию Грина
Опр: Пусть ![]() - односвязная область с границей
- односвязная область с границей ![]() . Функция Грина в
. Функция Грина в ![]() есть
есть ![]() , где
, где ![]() - конформное отображение
- конформное отображение ![]() на
на ![]() , переводящее
, переводящее ![]() в
в ![]() .
.
Утверждение: Если задана непрерывная функция ![]() на
на ![]() , то решение задачи Дирихле
, то решение задачи Дирихле ![]() записывается, как
записывается, как ![]() , где
, где ![]() - внутренняя нормаль к
- внутренняя нормаль к ![]() в точке
в точке ![]() , и
, и ![]() - элемент длины дуги.
- элемент длины дуги.
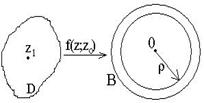 Схема доказательства: Пусть существует решение задачи Дирихле
Схема доказательства: Пусть существует решение задачи Дирихле ![]() в
в ![]() . Тогда
. Тогда ![]() - по свойству композиции является гармонической функцией в
- по свойству композиции является гармонической функцией в ![]() . Пусть
. Пусть ![]() , тогда по теореме о среднем:
, тогда по теореме о среднем:  , где
, где ![]() ,
, ![]() ,
, ![]() - элемент
- элемент ![]() ,
, ![]() - элемент
- элемент ![]() . В силу того, что
. В силу того, что ![]() и по геометрическому смыслу модуля производной, получаем:
и по геометрическому смыслу модуля производной, получаем: ![]() (минус появляется из-за того, что
(минус появляется из-за того, что ![]() - внутренняя нормаль), тогда
- внутренняя нормаль), тогда ![]() :
: 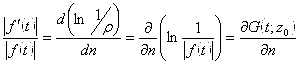 . Отсюда
. Отсюда ![]() получаем следующее равенство:
получаем следующее равенство: ![]() . При
. При ![]() под знаком интеграла
под знаком интеграла ![]() и в пределе, получаем:
и в пределе, получаем: ![]() . Утверждение доказано.
. Утверждение доказано.
| < Предыдущая | Следующая > |
|---|