70. Принцип граничного соответствия

Теорема: Пусть - жордановы области в и - функция, аналитическая в . Пусть . Если осуществляет гомеоморфизм границ , сохраняющий направление обхода, то - конформное отображение.

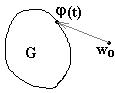Доказательство: 1) Покажем, что область . Допустим, что . Пусть , , и является аналитической в . По принципу аргумента для имеем: , где и - число нулей в . Но так как (см. рисунок). Противоречие. Следовательно, .

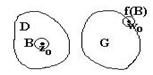2) Покажем, что . Пусть и , , . Тогда - кружочек (см. рисунок), такой, что , тогда , так как в силу того, что - аналитическая и - открытое - открытое (по топологическому свойству аналитических функций), следовательно, . Противоречие с пунктом (1). .

3) Покажем, что . Рассмотрим функцию , которая является аналитической и , где - число нулей функции . Но в силу того, что , в которой . Теорема доказана.

< Предыдущая		Следующая >