68. Аналитические дуги и теорема Шварца

Опр: Жорданова дуга называется Аналитической, если существует аналитическая комплекснозначная функция такая, что , которая называется Аналитической параметризацией Дуги и - гомеоморфизм, и (Условие регулярности).

Лемма (о распрямлении аналитической дуги): Пусть - параметризация аналитической дуги , тогда - область, симметричная относительно вещественной оси и - аналитическое продолжение функции в область , которая является конформным отображением.

Схема доказательства: - требуемая аналитическая в такая, что это выполняется в некоторой окрестности . Область образуется этими окрестностями.

Теорема Шварца (об аналитическом продолжении через дугу): Пусть - жорданова область, - аналитическая дуга на границе области. Пусть - аналитическая функция в и , где - некоторая аналитическая дуга. Тогда существует область такая, что и функция , аналитическая в такая, что .

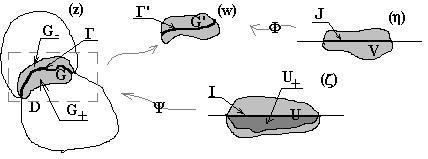Доказательство: По лемме о конформном распрямлении аналитической дуги - отрезок в плоскости и - симметричная относительно вещественной оси окрестность, и отображение такое, что И, пожалуй, всё. Аналогично для существуют отрезок в плоскости и симметричная относительно вещественной оси окрестность , и отображение (см. рисунок). Так как - конформное, то пусть - две части области , внутри и вне области соответственно. Пусть - аналитическая функция, заданная , где . Тогда и выполнены условия принципа симметрии Римана-Шварца можно продолжить до аналитической функции , которая определена в области , где - симметричная область для относительно и - аналитическая функция в , и . Тогда - аналитическая функция, заданная в . При этом , так как . Отсюда следует, что функция корректно определена и является аналитической в и . Теорема доказана.