56. Разложение функций и
периодическая с периодом 
, особые точки 
(полюсы 2 порядка).
Утв: 
выполняется равенство 
.
Доказательство: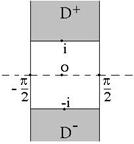
Главная часть лорановского разложения 
в точке 
: 
, 
, 
- главная часть. 
(или т. к. - четная). Отсюда главная часть в равна 
, в равна 
. Рассмотрим ряд 
. Пусть 
, построим круг 
. 
, 
, отсюда: 
, тогда 
. Ряд 
сходится, 
- сходится равномерно на любом компакте в 
и функция 
аналитична, периодична с периодом и имеет особые точки и в окрестности 
она имеет вид: 
. Рассмотрим 
. Для нее точки являются устранимыми, она аналитична и периодична с периодом на всей 
. Рассмотрим 
в полосе 
и найдем 
. Пусть 
(см. рисунок). Покажем, что 
и 
. Отсюда будет следовать, что 
и в силу периодичности будет ограниченной на и по теореме Лиувилля 
.
1) 
, 
. Если расписать это через 
, то легко показать, что 
. Отсюда .
2) 
, зададим 
. Ряд 
сходится равномерно, так как он мажорирует во всей полосе с 
. Поэтому 
, т. ч: 
и 
, откуда следует, что 
. В силу произвольности 
. Это значит в силу вышеприведенных рассуждений, что 
и 
. Утверждение доказано.
Далее:
. 
, где легко заметить, что 
. И получаем 
. Полученные разложения имеют место на всей комплексной плоскости .
| < Предыдущая | Следующая > |
|---|
