52. Теорема Руше
Теорема: Пусть область ![]() ограничена кусочно-гладкой границей
ограничена кусочно-гладкой границей ![]() и функции
и функции ![]() и
и ![]() аналитичны в области
аналитичны в области ![]() . Если
. Если ![]() выполняется неравенство
выполняется неравенство ![]() , то функции
, то функции ![]() и
и ![]() имеют в
имеют в ![]() одинаковое число нулей с учетом кратности, то есть
одинаковое число нулей с учетом кратности, то есть ![]() .
.
 Доказательство: Из условия
Доказательство: Из условия ![]() следует, что
следует, что ![]() на
на ![]() , т. к. слева стоит неотрицательная величина и строгое неравенство. А также
, т. к. слева стоит неотрицательная величина и строгое неравенство. А также ![]() на
на ![]() в силу того, что неравенство строгое. Отсюда следует в силу аналитичности и ограниченности
в силу того, что неравенство строгое. Отсюда следует в силу аналитичности и ограниченности ![]() , что эти функции имеют конечное число изолированных нулей внутри
, что эти функции имеют конечное число изолированных нулей внутри ![]() . Рассмотрим функцию
. Рассмотрим функцию ![]() , которая будет аналитичной в некоторой окрестности
, которая будет аналитичной в некоторой окрестности ![]() . Для этой функции нули
. Для этой функции нули ![]() являются нулями, а нули
являются нулями, а нули ![]() являются полюсами.
являются полюсами.
Таким образом для ![]() имеет место принцип аргумента. В силу условия теоремы:
имеет место принцип аргумента. В силу условия теоремы:![]() , или
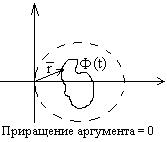
, или ![]() . Это неравенство означает, что
. Это неравенство означает, что ![]() (см. рисунок). В силу этого, приращение аргумента
(см. рисунок). В силу этого, приращение аргумента ![]() . Отсюда сразу следует утверждение теоремы. Теорема доказана.
. Отсюда сразу следует утверждение теоремы. Теорема доказана.
Применение этой теоремы: Докажем основную теорему алгебры о том, что многолчен ![]() степени
степени ![]() имеет ровно
имеет ровно ![]() корней с учетом кратности.
корней с учетом кратности.
Доказательство: Многочлены ![]() аналитичны на всей
аналитичны на всей ![]() .
.
![]()
![]()
![]() . То есть все нули многочлена лежат в круге
. То есть все нули многочлена лежат в круге ![]() . Пусть теперь
. Пусть теперь ![]() . Тогда
. Тогда  , следовательно
, следовательно ![]() , такой, что
, такой, что ![]() эта дробь будет меньше единицы, а это означает, что будет выполняться условие теоремы Руше, где
эта дробь будет меньше единицы, а это означает, что будет выполняться условие теоремы Руше, где ![]() . Функция
. Функция ![]() имеет в круге
имеет в круге ![]() один корень
один корень ![]() кратности
кратности ![]() , а все корни
, а все корни ![]() лежат в круге
лежат в круге ![]() (по построению). Теорема доказана.
(по построению). Теорема доказана.
| < Предыдущая | Следующая > |
|---|