51. Принцип аргумента

Пусть ![]() - «воротниковая» окрестность кривой
- «воротниковая» окрестность кривой ![]() , где
, где ![]() - некоторая область и
- некоторая область и ![]() аналитична и не равна нулю в
аналитична и не равна нулю в ![]() . Зафиксируем точку
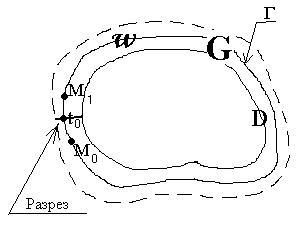
. Зафиксируем точку ![]() и проведем через нее разрез
и проведем через нее разрез ![]() в виде кусочно-гладкой дуги
в виде кусочно-гладкой дуги ![]() (см. рисунок). Тогда
(см. рисунок). Тогда ![]() - односвязная область, в которой функция
- односвязная область, в которой функция ![]() аналитична в силу перечисленных условий. По теореме о существовании первообразной в односвязной области и в силу того, что
аналитична в силу перечисленных условий. По теореме о существовании первообразной в односвязной области и в силу того, что ![]()
![]()
![]() - первообразная для
- первообразная для ![]() . Таким образом мы выделяем непрерывную ветвь логарифма. И по формуле Ньютона-Лейбница:
. Таким образом мы выделяем непрерывную ветвь логарифма. И по формуле Ньютона-Лейбница: ![]() . Теперь, устремив
. Теперь, устремив ![]() , мы получаем:
, мы получаем: ![]() , где первое слагаемое равно нулю в силу того, что
, где первое слагаемое равно нулю в силу того, что ![]() - однозначная функция. В силу формулы логарифмического вычета, получаем:
- однозначная функция. В силу формулы логарифмического вычета, получаем: ![]() . Отсюда сразу получаем Принцип аргумента:
. Отсюда сразу получаем Принцип аргумента: ![]() .
.
Геометрический смысл этого принципа показан на рисунке. Величина, стоящая в числителе есть число полных оборотов точки-образа вокруг нуля при одном полном обходе точки прообраза по границе области ![]() .
.
Пример: Пусть в ![]() - функция имеет в круге
- функция имеет в круге ![]() один нуль третьего порядка
один нуль третьего порядка ![]() , тогда в образе границы круга будет окружность радиуса 1, которая обходится ровно три раза.
, тогда в образе границы круга будет окружность радиуса 1, которая обходится ровно три раза.
| < Предыдущая | Следующая > |
|---|