47. Понятие интеграла в смысле главного значения
 Пусть
Пусть ![]() - кусочно-гладкая кривая и функция
- кусочно-гладкая кривая и функция ![]() непрерывна на
непрерывна на ![]() , тогда
, тогда ![]() - несобственный интеграл. Пусть
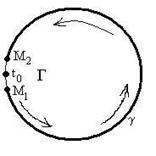
- несобственный интеграл. Пусть ![]() с разных сторон,
с разных сторон, ![]() и
и ![]() - дуга от
- дуга от ![]() до
до ![]() (см. рисунок).
(см. рисунок).
Опр: Тогда ![]() , рассмотрим предел
, рассмотрим предел ![]() , если этот предел существует при любых стремлениях
, если этот предел существует при любых стремлениях ![]() и
и ![]() , независимых друг от друга, то говорят, что интеграл
, независимых друг от друга, то говорят, что интеграл  Сходится, в противном случае говорят, что интеграл Расходится.
Сходится, в противном случае говорят, что интеграл Расходится.
Опр: Пусть ![]() , тогда если существует предел
, тогда если существует предел ![]() , то он называется Главным значением интеграла
, то он называется Главным значением интеграла ![]() и обозначается, как
и обозначается, как ![]() .
.
Замечание: Главное значение может существовать даже если интеграл расходится.
Пример: ![]() расходится, но
расходится, но  .
.
В случае, когда ![]() ,
, ![]() - кусочно-гладкая кривая в
- кусочно-гладкая кривая в ![]() и
и ![]() непрерывна на
непрерывна на ![]() , обозначим
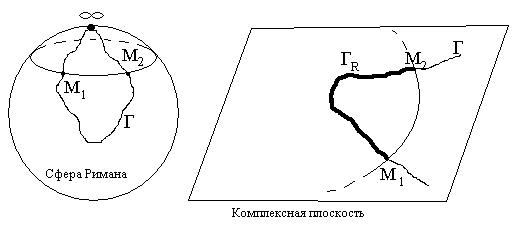
, обозначим ![]() (см. рисунок) и главным значением интеграла будет:
(см. рисунок) и главным значением интеграла будет: ![]() .
.
| < Предыдущая | Следующая > |
|---|