44. Вычеты аналитической функции

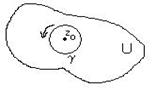
Пусть - регулярная или изолированная точка для . Тогда , где не зависит от выбора .

Опр: Вычетом функции в точке называется величина .

Замечание: Если аналитична в окрестности точки , то по теореме Коши . Это же выполняется в случае, когда является устранимой ОТ (доопределив в ней, получаем функцию, аналитичную в окрестности ).

Утв: Пусть - изолированная ОТ функции , тогда , где - коэффициент лорановского разложения функции в проколотой окрестности точки .

Доказательство: По определению: . Утверждение доказано.

Если - изолированная ОТ, тогда для достаточно большого : - черта означает отрицательное направление интегрирования. Если разложить функцию в ряд Лорана в проколотой окрестности бесконечности: , где , то нетрудно убедиться, что . Минус появляется из-за различных направлений интегрирования.

Замечание: Если является устранимой ОТ, то отсюда Не следует, что .

< Предыдущая		Следующая >