15. Принцип симметрии для ДЛО

Утверждение: и симметричны относительно обобщенной окружности - обобщенная окружность, проходящая через эти точки, пересекает под прямым углом.

Доказательство:

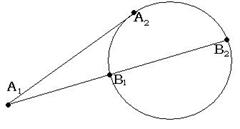
Из элементарной геометрии:

В дальнейшем это равенство будет использовано..

Пусть и симметричны относительно .

Рассмотрим два случая:

1) - прямая. Тогда эта прямая будет разбивать любую окружность, проходящую через и пополам. Это легко установить элементарными геометрическими соотношениями. Значит эта прямая пройдет через диаметр и будет пересекать окружность под прямым углом.

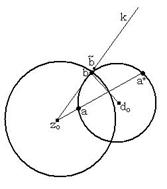2) - окружность. . Пусть - обобщенная окружность через и . И - одна из точек пересечения. Пусть - касательная к из центра . И пусть она касается окружности не в точке , а в точке .

Из вышеупомянутой геометрической формулы и симметрии и :

Последнее раветство имеет место в силу того, что . Отсюда в силу того, что и лежат на одном радиус-луче .

Теорема доказана.

Теорема: Пусть - ДЛО и - симметричны относительно обобщенной окружности . Тогда симметричны относительно .

Доказательство: Проведем через обобщенную окружность .

В силу кругового свойства ДЛО - тоже обобщенная окружность. По предыдущему утверждению легко видеть: . Далее:; .

В силу конформности ДЛО прямой угол пересечения сохраняется. Аналогичны рассуждения для точки . Далее по предыдущему утверждению следует то, что требовалось.

Теорема доказана.

< Предыдущая		Следующая >