04. Компактные множества

Опр: Пусть - топологическое пространство и множество . Семейство {, где , - открытое в } называется Открытым покрытием множества , если . называется Компактным, если из любого его открытого покрытия можно выделить конечное подпокрытие. То есть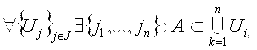

Утв: Множество является копмактным замкнуто и ограничено.

След: - компактно - компактно. не является компактным - гомеоморфизм.

Утв: Непрееывный образ компакта есть компакт.

Теорема о вложенных компактах: Пусть в хаусдорфовом топологическом пространстве задана последовательность непустых компактов: Тогда непусто и является компактом.

Доказательство: Пусть пусто. Тогда имеем: .

Так как пространство хаусдорфово, - открытое, то существуе открытая окрестность точки такая, что . - открытое покрытие . В силу компактности . И в силу предыдущего рассуждения . Пусть . Тогда получаем: . Противоречие. Теорема доказана.

Теорема (аналог теоремы Вейерштрасса): Если - компакт в и - вещественная непрерывная функция, то

Опр: Пусть и - метрические пространства и . Отображение называется Равномерно непрерывным на , если выполняется следующее:

Теорема (аналог теоремы Кантора-Гейне): Если - компакт в и - непрерывно, то - равномерно непрерывно.

Упр: Доказать, что в хаусдорфовом пространстве любое компактное множество замкнуто.

Упр: Доказать, что в любом хаусдорфовом пространстве одноэлементное множество является компактным.

Упр: Пусть - компакт в топологическом пространстве . Доказать, что любое бесконечное множество имеет хотя бы одну предельную точку в .

Упр: Пусть - компакт в топологическом пространстве . - хаусдорфово топологическое пространство - взаимооднозначно и непрерывно. Показать непрерывность . (т. е. показать, что - гомеоморфизм).

< Предыдущая		Следующая >