01. Комплексные числа
Для пары ![]() Комплексным числом называется число вида
Комплексным числом называется число вида ![]() (
(![]() называется вещественной частью и обозначается
называется вещественной частью и обозначается ![]() ,
, ![]() называется мнимой частью и обозначается
называется мнимой частью и обозначается ![]() ). Данная запись называется Алгебраической формой записи комплексного числа. Элемент i называется Мнимой единицей и обладает свойством:
). Данная запись называется Алгебраической формой записи комплексного числа. Элемент i называется Мнимой единицей и обладает свойством: ![]() . Каждому комплексному числа в соответствие можно сопоставить пару чисел
. Каждому комплексному числа в соответствие можно сопоставить пару чисел ![]() или вектор с координатами
или вектор с координатами ![]() . Свойство элемента i легко вывести из правила умножения комплексных чисел:
. Свойство элемента i легко вывести из правила умножения комплексных чисел:
![]()
Для каждого комплексного числа ![]() существует Комплексно-сопряженное число
существует Комплексно-сопряженное число ![]() . Легко видеть, что произведение комплексного числа на комплексно-сопряженное к нему в результате дает вещественное число.
. Легко видеть, что произведение комплексного числа на комплексно-сопряженное к нему в результате дает вещественное число.
Модулем комплексного числа ![]() Называется вещественное неотрицательное число, которое задается следующей формулой:
Называется вещественное неотрицательное число, которое задается следующей формулой: ![]() .
.
При изображении комплексного числа на комплексной плоскости, в соответствие ему ставят вектор с координатами ![]() :
:
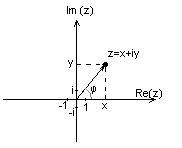 Легко видеть, что модуль числа
Легко видеть, что модуль числа ![]() Есть длина вектора
Есть длина вектора ![]() .
.
Угол ![]() Между положительным направлением вещественной оси и вектором
Между положительным направлением вещественной оси и вектором ![]() Называется Главной частью аргумента
Называется Главной частью аргумента ![]() , он обозначается как
, он обозначается как ![]() и принимает значения
и принимает значения ![]() .
.
Аргумент коплексного числа есть многозначная функция, заданная следующей формулой: ![]() .
.
Пусть ![]() , тогда имеет место равенство:
, тогда имеет место равенство:
![]()
Предпоследняя и последняя части этой формулы называются соответственно Тригонометрической и экспоненциальной формами записи комплексного числа.
Легко проверить следующие свойства комплексных чисел:
Модуль произведения двух комплексных чисел равен произведению модулей множителей, а аргумент произведения равен сумме аргументов множителей. Модуль частного двух комплексных чисел равен отношению соответствующих модулей, а аргумент частного равен разности аргументов.| Следующая > |
|---|