02. Подходящие дроби. Их свойства

Задаче разложения обыкновенной дроби в непрерывную дробь противостоит обратная задача – обращения или свертывания цепной дроби в простую дробь .

При этом основную роль играют дроби вида:

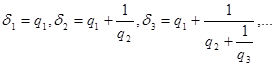или

которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа .

Заметим, что ==. Считается, что подходящая дробь имеет порядок k.

Прежде чем приступить к вычислению подходящих дробей заметим, что переходит в , если в первой заменить выражением .

Имеем ,

,

, …,

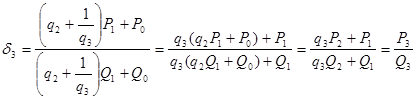При этом принимается, что , , , , , и так далее.

Закономерность, которую мы замечаем в построении формулы для (ее числителя и знаменателя ), сохраняется при переходе к и сохранится также при переходе от k к (k+1).

Поэтому, на основании принципа математической индукции, для любого k, где , имеем

(1),

Причем (2)

(3)

Далее, говоря о подходящих дробях (в свернутом виде), мы будем иметь в виду их форму .

Соотношения (1) являются рекуррентными формулами для вычисления подходящих дробей, а также их числителей и знаменателей. Из формул для числителя и знаменателя сразу видно, что при увеличении k они возрастают. Последовательное вычисление числителей и знаменателей подходящих дробей по формулам (2) и (3) удобно располагать по схеме:

				…				…
				…				…
				…				…

Пример: Найти подходящие дроби к цепной дроби (2, 2, 1, 3, 1, 1, 4, 3).

	2	2	1	3	1	1	4	3
	2	5	7	26	33	59	269	866
	1	2	3	11	14	25	114	367

Подходящие дроби () равны соответственно ; ; ; ; ; ; ; .

Практически нахождение неполных частных и подходящих дробей удобно объединить в одну краткую схему, которую приведем для =(2, 3, 1, 4, 2)

.

А сейчас рассмотрим ряд свойств подходящих дробей.

Теорема 1. При k=1, 2, …, n выполняется равенство

Д о к а з а т е л ь с т в о: Проведем индукцию по k:

При k=1 равенство справедливо, так как .

Пусть это равенство верно при некотором k=n ().

Докажем справедливость равенства при k=n+1.

, то есть равенство верно при k=n+1.

Согласно принципу полной математической индукции равенство верно для всех k().

Теорема 2 Числитель и знаменатель любой подходящей дроби – взаимно простые числа, то есть всякая k–подходящая дробь несократима.

Д о к а з а т е л ь с т в о. Докажем это свойство методом от противного. По предыдущему свойству имеем .

Пусть , то есть , тогда из равенства следует, что делится на без остатка, что невозможно. Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть .

Теорема 3. При

1) ()

2) ()

Д о к а з а т е л ь с т в о: Первое соотношение можно получить из равенства , доказанного выше, путем деления обеих частей на . Получаем

, что и требовалось доказать.

Докажем второе соотношение.

.

Теорема 4. Знаменатели подходящих дробей к цепной дроби, начиная с первого, образуют монотонно возрастающую последовательность, то есть 1=.

Д о к а з а т е л ь с т в о: , , так что и положительны.

Соотношение () (*) показывает, что и все следующие знаменатели , , …, положительны. При , поскольку тогда , из (*) получаем

, что и требовалось доказать.

Теорема 5. Нечетные подходящие дроби образуют возрастающую, а четные подходящие дроби – убывающую последовательность:

;

.

Две подходящие дроби и , у которых номер отличается на единицу, будем называть соседними.

Теорема 6. Из двух соседних подходящих дробей четная дробь всегда больше нечетной.

Д о к а з а т е л ь с т в о: По уже доказанному выше свойству имеем:

.

Если k – четное, то

Если k – нечетное, то

Значит, из двух соседних дробей и четная всегда больше нечетной, что и требовалось доказать.

Теорема 7. Расстояние между двумя соседними подходящими дробями .

Д о к а з а т е л ь с т в о: Так как , то , что и требовалось доказать.

< Предыдущая		Следующая >