093. Seasonal Variation

Many businesses experience seasonal variations in the level of their activity. Changes in weather and climate affect business conditions in agriculture and construction, as well as related industries such as farm implements and timber. Many commodities, such as swimwear and snow skis are influenced by changes in the season. Artificial seasons based on social customs, including Christmas, June weddings, and May graduations, have an impact on business activity. Thanksgiving and Easter affect the poultry and egg industries.

Seasons do not have to be as long as those implied above. Organized stock exchanges find that trading is heavier on Fridays and Mondays than it is on other weekdays. Here, the “season” is a single day.

The study of seasonal fluctuations lends much to our ability to evaluate and understand business behavior. The ultimate aim is to determine a seasonal index, which can be used to analyze and predict business activity.

The data in Table 8.7 show monthly profits for Vinnie’s Video Village. A superficial examination reveals that profits seem to be higher during the summer months when school is out, and lower at other times of the year. This suggests the presence of seasonal factors.

Table 8.7 - Seasonal Fluctuations in Vinnie`s Profits

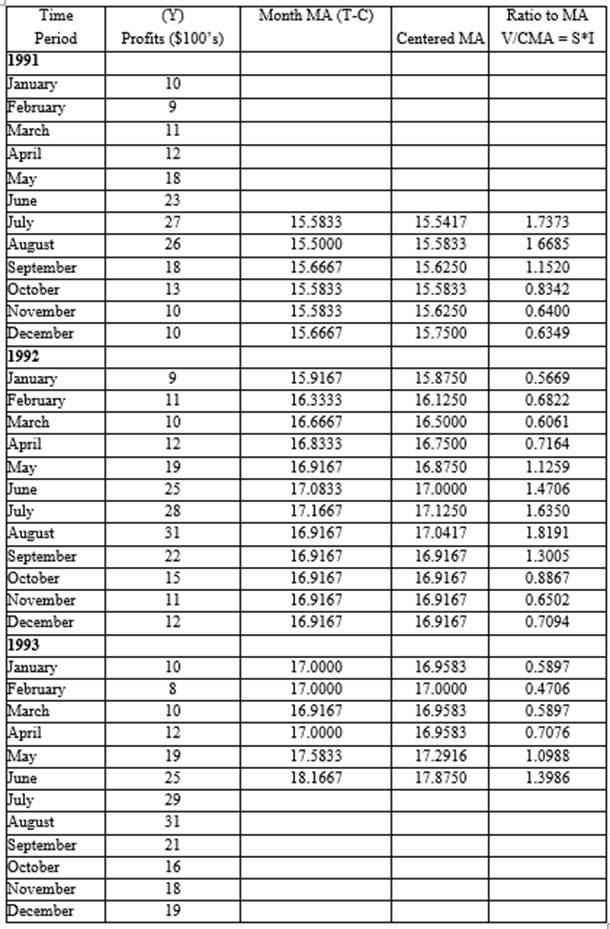
The first step in developing a seasonal index is to calculate a centered moving average. Since Vinnie’s profits tend to fluctuate over the course of the year, and monthly data are used, a 12-period (month) moving average should be calculated. If activity on organized stock exchanges has to be analyzed, the daily data should be used and a five-period (for the five business days) moving average has to be constructed.

Table 8.7 shows the 12-month moving average and the centered moving average (CMA). As noted, the moving average eliminates recurring seasonal movements as well as any random effects over the course of the year. Thus, given a multiplicative model Y = T * C * S * I, the moving average eliminates S and I and contains only T and C. That is, MA = T * C.

It is now possible to calculate the Ratio to moving average. To do this, divide the original series value Y by the moving average. The result produces the S and I components of the time series.

By dividing the time-series values by the moving average the I component will be removed shortly.

Ratio to Moving Average. By dividing the original time-series data by the moving average, the ratio to moving average is obtained, which contains the S and I components.

A Mean ratio to moving average is calculated for each month as shown in Table 8.8. These mean ratios are then normalized to produce the seasonal indexes. The purpose of this normalization procedure is to ensure that the seasonal indexes will sum to 12, since a 12-period moving average is used. This is accomplished by multiplying each mean by a Normalization ratio, which is the ratio of 12 to the sum of the means. Notice in Table 8.8 that the sum of the means of the ratio to moving averages is 11.8454. Thus, the normalization ratio is

Then the seasonal indexes are found by multiplying each mean by 1.01305. This normalization removes the irregular component, leaving only the seasonal factor.

Uses of the Seasonal Index

1. After going to all the trouble of calculating these seasonal indexes, you will be glad to know that they are put to vital use. For example, the seasonal index for a particular month indicates How that month performs relative to the year as a whole.

Table 8.8 - Seasonal Indexes for Vinnie`s Profits

Month	1991	1992	1993	Mean Ratio to MA	Seasonal Index
January		0.5669	0.5897	0.5783	0.5858
February		0.6822	0.4706	0.5764	0.5839
March		0.6061	0.5897	0.5979	0.6057
April		0.7164	0.7076	0.7120	0.7213
May		1.1259	1.0988	1.1124	1.1269
June		1.4706	1.3986	1.4346	1.4533
July	1.7373	1.6350		1.6861	1.7082
August	1.6685	1.8191		1.7438	1.7665
September	1.1520	1.3005		1.2262	1 2422
October	0.8342	0.8867		0.8605	0.8717
November	0.6400	0.6502		0.6451	0.6535
December	0.6349	0.7094		0.6721	0.6809
				11.8454	11.9999 12

The index of 0.5858 for January tells Vinnie that profits in January are only 58.58 percent of the average for the full year. Profits are 41.42 percent (1.000 — 0.5858) below the year’s monthly average.

2. Perhaps more importantly, the indexes can be used to Deseasonalize data. This has the effect of removing seasonal variation from a series to determine what the values would be in the absence of seasonal variations. It yields the average value per month that would occur if there were no seasonal changes. The deseasonalized value is found by dividing the actual value during the month by the seasonal index in that month. For example, in January 1991, the deseasonalized value is

=17.07.

In other words, if Vinnie’s business was not subject to seasonal variation, profits in January 1991 would have been $1,707.

Deseasonalized values are also called Seasonally adjusted because they tell us what the values would be if we adjust for seasonal influences. The classic example involves unemployment rates. Since unemployment is usually higher in May than most other months due to school dismissals and the influx of many teenagers into the job market, the seasonal index for May will be greater than 1. If actual unemployment in May is 7.2 percent and the index is, say, 1.103, the deseasonalized, or seasonally adjusted, rate of unemployment is 7.2/1.103 = 6.53 percent. This is not to say that unemployment was 6.53 percent. (It was actually 7.2 percent.) But when we adjust for seasonal forces, which typically inflate the rate of unemployment in May, the deseasonalized rate is lower. In this manner a measure or index of seasonal variation can be used to determine if the change in some series is more or less than what might be expected given the typical seasonal behavior.

Deseasonalized Values Deseasonalized values are obtained by dividing the actual values by their respective seasonal indexes. They reflect what the variable would be if we adjusted for seasonal influence.

3. The reverse is possible, in that the seasonal index can be used to Seasonalize data To get a better picture of what any one month might generate in profits. Assume Vinnie felt that profits might total 190 during the year. Without any seasonalization it might be argued that each month would generate 190/12 = 15.83, or $1,583 in profits. However, Vinnie knows that monthly variations will occur. He could seasonalize the data to determine the extent of that monthly variation by multiplying 15.83 by the seasonal index. He knows that in January profits tend to be 58.58 percent of the yearly total. His estimate of profits for January is (15.83X0.5858) = 9.27, or $927.

Or perhaps Vinnie is working with the trend equation which, given the data, is

Yt=13.85+0.167t.

The forecast for January 1994, the 37th time period, is

Yt=13.85+0.167(37) =20.31.

This doesn’t account for the seasonal lows that occur in January. The value can be seasonalized by multiplying by the seasonal index for January, yielding (20)*(0.5858) = 11.73, which is probably more accurately reflects profits during that month.

< Предыдущая		Следующая >