081. Testing Inferences about the Population Regression Coefficient. A Confidence interval for β1

If the slope of the actual but unknown population regression line is zero, there is no relationship between X and Y. but due to the luck of the draw in the sample, the researcher can select sample data that suggest a relationship. It might happen as shown in Figure 7.14

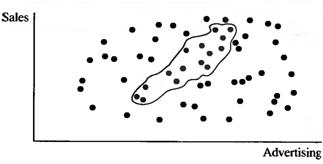
Figure 7.14 – A Possible Pattern of Population Data for Hop Scotch Airlines

As it can be plainly seen, the sample regression would be positively sloped, B1 > 0, and a relationship would be suggested by OLS. It is therefore often a wise practice to test the hypothesis that β1 = 0 given B1 ≠ 0. The test involves

H0 : β1 = 0;

Hα : β1 ≠ 0;

And uses a T-statistics defined as

, (7.6.7)

, (7.6.8)

Where is the standard error of the regression coefficient B1 and it measures the variation in the regression coefficient;

is the standard error of the estimate.

A critical value for t is obtained from the table and compared with the t-value calculated from the sample by using Formula (7.6.7).

A confidence interval for β1 is calculated then by using Formula (7.6.9)

C. I. for β1 = B1 ± t, (7.6.9)

Where the t-statistics has n-2 degrees of freedom

< Предыдущая		Следующая >