064. Adjusting the Sample Size

Another common Method of generating a narrower interval is to take a larger sample. It has been repeatedly emphasized that large samples will reduce the expected error and are more likely to produce an estimate closer to the true value of the parameter. Therefore, the researcher can retain a given level of confidence and still reduce the width of the interval.

Return to Example 6.5. In a sample of N = 350, 22 percent of the CEOs were outsiders. The 99 percent confidence interval was 16.3 percent to 27.7 percent In order to narrow the interval and yet retain the 99 percent level of confidence, it is necessary to increase the sample size. Assume that in a sample of N = 700, 22 percent are found to be outsiders. The sample proportion of 22 percent is held constant to ensure that the only sample size is changed. The 99 percent confidence interval is then

Sp =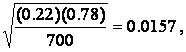

C. I. for π = 0.22 + (2.58)(0.0157) =.022+0.041,

0.179 < π < 0.261.

The results of increasing the size of the sample are shown in Figure 6.6.

A b

Figure 6.6 – Comparing Sample Sizes: A – Sample Size N = 350;

B – Sample Size N = 700

Notice that the larger sample size produced a smaller standard error, Sp. The earlier example with N = 350 produced a standard error of 0.022, while this sample size of 700 resulted in a standard error of only 0.0157. The 99 percent confidence interval is therefore contained within a narrower range.

There is again, however, a cost associated with producing this more precise interval – in the form of the time and expense required to collect a larger sample. This additional cost must be judged against the higher degree of precision.

< Предыдущая		Следующая >