063. Adjusting the Level of Confidence

By the mere nature of confidence intervals, accepting a lower level of confidence in the interval will generate a more precise, narrower interval.

Example 6.5. Headhunters in Paradise. Executive search firms specialize in helping corporations locate and secure top-level management talent. Called “headhunters,” these firms are responsible for the placement of many of the nation’s top CEOs. Business Week recently reported on the “efforts by headhunters to place executives in a heavenly corporate setting.” A source was quoted in the story as saying that “one out of every four CEOs is an outsider – an executive with less than five years at the company he runs.”

1) If, in a sample of 350 US corporations, 77 have outsider CEOs, would a 99 percent confidence interval support the quote?

Solution:

P =

Sp =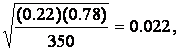

C. I. for π = p + Zsp=0.22 + (2.58)(0.022),

0.163 < π < 0.277.

Interpretation: We are confident at the 99 percent level that between 16.3 percent and 27.7 percent of US corporations have outside CEOs. The quote is supported by these findings, since 25 percent is contained within the interval.

2) If we were willing to accept a 10 percent probability of error, by constructing a 90 percent interval, we would have

C. I. for = 0.22 + (1.65)(0.022) = 0.22 + 0.036,

0.184 < < 0.256.

The effect of decreasing the level of confidence from 99 percent to 90 percent is shown in Figure 6.5.

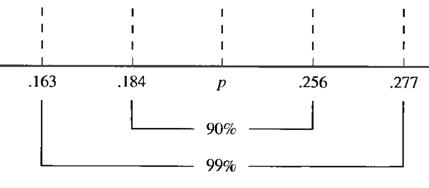
Figure 6.5 – Comparing 99 Percent and 90 Percent Confidence Intervals

The estimate now places π between 18.4 percent and 25.6 percent. This is certainly a narrower interval, but the aforementioned cost is a loss of confidence in the interval and a marked increase in the probability of error. It is up to the researcher, based on how critical his or her work is, to determine what probability of error can be tolerated. A trade-off must be made.

< Предыдущая		Следующая >