046. The Exponential Distribution

The Exponential distribution is a continuous distribution that measures the passage of time between events. It can measure the time lapse as

1. The time that passes between two successive arrivals (people, trucks, telephone calls, etc.);

2. The amount of time that it takes to complete one action, such as serving one customer, loading one truck, handling one call.

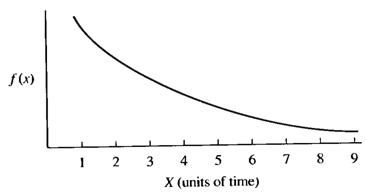
Figure 4.6 – An Exponential Probability Function

The Figure 4.6 shows That the larger the value of the random variable, as measured in units of elapsed time, the less likely it is to occur.

If the Arrival process is Poison-distributed, then the Lapse of time Between arrivals Is exponentially distributed. Let μ be the mean number of arrivals in a given time period, and let μ* be the mean lapse of time between arrivals. Then,

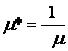. (4.21)

For Example, if an average of four trucks arrive every hour at the loading dock (μ = 4), then, on average, one truck arrives every 0.25 hour. That is,

hour.

The probability that no more than T units of time elapse between successive occurrences is

, (4.22)

Where μ is the mean rate of occurrence; E = 2.71828 is the base of natural logarithm system.

The exponential distribution has a very common and useful application in business in the evaluation of waiting lines, or queues. Many business operations involve lines. Customers queue up for service, telephone calls come into a switchboard, trucks arrive at the loading dock, and machines break down and must be repaired.

Let Λ be the average rate at which units arrive for service per unit of time, μ the average number of units that can be serviced in that same time unit. Then a Queuing system can be evaluated as

,

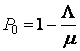Where P0 is the probability the system is idle; that is, there are no units in the system;

,

Where Pn is the probability N units are in the system;

,

Where L is the average number of units in the system (those waiting for service plus the one receiving the service);

,

Where W is the average time a unit spends in the system waiting for service and receiving that service (waiting time plus service time);

,

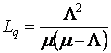Where is the average number of units waiting for service;

,

Where is the average time spent in the queue waiting for service to begin.

< Предыдущая		Следующая >